Question

【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，动点M从点A出发，以每秒1个单位长度的速度沿AB向点B匀速运动；同时，动点N从点B出发，以每秒3个单位长度的速度沿BA向点A匀速运动，过线段MN的中点G作边AB的垂线，垂足为点G，交△ABC的另一边于点P，连接PM，PN，当点N运动到点A时，M，N两点同时停止运动，设运动时间为t秒．

（1）当t=秒时，动点M，N相遇
（2）设△PMN的面积为S，求S与t之间的函数关系式
（3）取线段PM的中点K，连接KA，KC，在整个运动过程中，△KAC的面积是否变化？若变化，直接写出它的最大值和最小值；若不变化，请说明理由．

Answer 1

【答案】
（1）2.5
（2）

解：过点C作CH⊥AB于H，

由S△ABC=ACBC=ABCH得，CH==4.8，

∴AH==3.6，BH=10﹣3.6=6.4．

∵当点N运动到点A时，M，N两点同时停止运动，∴0≤t≤．

当0≤t＜2.5时，点M在点N的左边，如图1、图2，

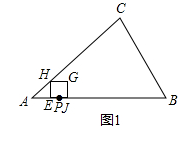
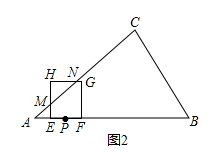
MN=AB﹣AM﹣BN=10﹣t﹣3t=10﹣4t．

∵点G是MN的中点，∴MG=MN=5﹣2t，

∴AG=AM+MG=t+5﹣2t=5﹣t，

∴BG=10﹣（5﹣t）=t+5．

当点P与点C重合时，点G与点H重合，

则有5﹣t=3.6，解得t=1.4．

当2.5＜t≤时，点M在点N右边，如图3，

∵MN=AM﹣AN=AM﹣（AB﹣BN）=t﹣（10﹣3t）=4t﹣10，

∴NG=MN=2t﹣5，

∴AG=AN+NG=10﹣3t+2t﹣5=5﹣t．

综上所述：①当0≤t≤1.4时，点M在点N的左边，点P在BC上，如图1，

此时MN=10﹣4t，BG=t+5，PG=BGtanB=（t+5）=t+，

∴S=MNPG=（10﹣4t）（t+）=﹣t2﹣t+；

②当1.4＜t＜2.5时，点M在点N的左边，点P在AC上，如图2，

此时MN=10﹣4t，AG=5﹣t，PG=AGtanA=（5﹣t）=﹣t，

∴S=MNPG=（10﹣4t）（﹣t）=t2﹣20t+；

③当2.5＜t≤时，点M在点N的右边，点P在AC上，如图3，

此时MN=4t﹣10，AG=5﹣t，PG=AGtanA=（5﹣t）=﹣t，

∴S=MNPG=（4t﹣10）（﹣t）=﹣t2+20t﹣；

∴S与t之间的函数关系式为S=；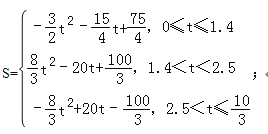

（3）

解：在整个运动过程中，△KAC的面积变化，最大值为4，最小值为．

提示：过点K作KD⊥AC于D，过点M作ME⊥AC于E．

①当0≤t≤1.4时，点P在BC上，如图4，

此时AM=t，BG=t+5，

∴EM=AMsin∠EAM=t=t，BP===t+，

∴CP=CB﹣BP=8﹣（t+）=﹣t+．

∵EM⊥AC，KD⊥AC，PC⊥AC，

∴EM∥DK∥CP．

∵K为PM的中点，∴D为EC中点，

∴DK=（CP+EM）=（﹣t++t）=﹣t+，

∴S△KAC=ACDK=×6×（﹣t+）=﹣t+，

∵﹣＜0，∴S△KAC随着t的增大而减小，

∴当t=0时，S△KAC取到最大值，最大值为，

当t=1.4时，S△KAC取到最小值，最小值为；

②当1.4＜t≤时，点P在AC上，如图5、图6，

同理可得：DK为△PEM的中位线，EM=t，

∴DK=EM=t，

∴S△KAC=ACDK=×6×t=t．

∵＞0，∴S△KAC随着t的增大而增大，

∴当t=1.4时，S△KAC取到最小值，最小值为；

当t=时，S△KAC取到最大值，最大值为×=4

综上所述：△KAC的面积的最大值为4，最小值为．

【解析】（1）根据勾股定理可得AB=10，若动点M、N相遇，则有t+3t=10，即可求出t的值；
（2）由于“点P在BC上”与“点P在点AC上”及“点M在点N的左边”与“点M在点N的右边”对应的MN、PG的表达式不同，S与t之间的函数关系式也就不同，因此需分情况讨论．只需先考虑临界位置（点P与点C重合，点M与点N重合、点N与点A重合）所对应的t的值，然后分三种情况（①0≤t≤1.4，②1.4＜t＜2.5，③2.5＜t≤）讨论，用t的代数式表示出MN和PG，就可解决问题；
（3）过点K作KD⊥AC于D，过点M作ME⊥AC于E，由于AC已知，要求△KAC的面积的最值，只需用t的代数式表示出DK，然后利用一次函数的增减性就可解决问题．
【考点精析】解答此题的关键在于理解平行线分线段成比例的相关知识，掌握三条平行线截两条直线，所得的对应线段成比例，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．