题目内容
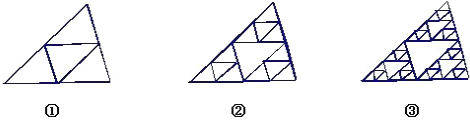
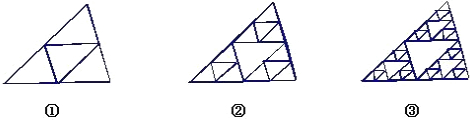
观察下列图形： 如果按这个规律一直排到第n个图形，请探究下列问题：
（1）设第n个图形和第n-1个图形中所有三角形的个数分别为an、an-1，问：它们之间有什么数量关系？请写出这个关系式。
（2）请你用含n的代数式来表示an，并证明你的结论。
（1）设第n个图形和第n-1个图形中所有三角形的个数分别为an、an-1，问：它们之间有什么数量关系？请写出这个关系式。
（2）请你用含n的代数式来表示an，并证明你的结论。
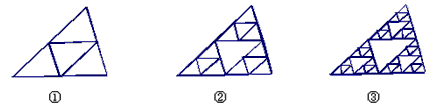
解：（1）按题中图形的排列规律可得：an =3an-1 +2
（2）由（1）得：an =3an-1 +2 ，an-1 =3an-2 +2 ，
两式相减得： an -an-1=3（an-1-an-2） ①
当n分别取3、4、5、…、n时，由①式可得下列（n-2）个等式：
a3-a2=3（a2-a1）, a4-a3=3（a3-a2）, a5-a4=3（a4-a3）,…, an-an-1=3（an-1-an-2）
显然an-an-1≠0，
以上（n-2）个等式的左右两边分别相乘约去相同的项后得：
an-an-1=3n-2 (a2-a1) ②
∵ a2-a1=17-5=12，由（1）又可知an-1=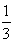
（an-2），
将它们代入②式即得：an=2×3n-1
（2）由（1）得：an =3an-1 +2 ，an-1 =3an-2 +2 ，
两式相减得： an -an-1=3（an-1-an-2） ①
当n分别取3、4、5、…、n时，由①式可得下列（n-2）个等式：
a3-a2=3（a2-a1）, a4-a3=3（a3-a2）, a5-a4=3（a4-a3）,…, an-an-1=3（an-1-an-2）
显然an-an-1≠0，
以上（n-2）个等式的左右两边分别相乘约去相同的项后得：
an-an-1=3n-2 (a2-a1) ②
∵ a2-a1=17-5=12，由（1）又可知an-1=
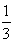（an-2），将它们代入②式即得：an=2×3n-1
练习册系列答案
相关题目
