题目内容
按如图所示的规律用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,并解答下面问题:
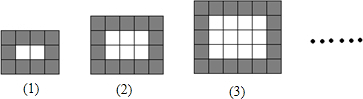
(1)将下表填写完整
(2)第(n)个图形中,共有黑色瓷砖
(3)如果每块黑色瓷砖12元每块白瓷砖10元,求购买铺设第(8)个图形所需瓷砖的费用;
(4)是否存在第(n)个图形,该图形所需白、黑瓷砖的总数为18325块?若存在,求出该图形的编号n;若不存在,请说明理由.

(1)将下表填写完整
| 图形编号 | (1) | (2) | (3) | (4) | … |
| 黑色瓷砖的块数 | 10 | 14 | 18 | 22 22 |
… |
| 白色瓷砖的块数 | 2 | 6 | 12 | 20 20 |
… |
4n+6
4n+6
块,共有白色瓷砖n(n+1)
n(n+1)
块;(用含n的代数式表示,答案直接写在题中横线上);(3)如果每块黑色瓷砖12元每块白瓷砖10元,求购买铺设第(8)个图形所需瓷砖的费用;
(4)是否存在第(n)个图形,该图形所需白、黑瓷砖的总数为18325块?若存在,求出该图形的编号n;若不存在,请说明理由.
分析:(1)根据图形直接数出填写即可;
(2)根据图形可以得出每一横行由(n+3)块瓷砖,每一竖列有(n+2)快瓷砖,第n个图形的白瓷砖的每行有(n+1)个,每列有n个,即可表示白瓷砖的数量,再让总数减去白瓷砖的数量即为黑瓷砖的数量;
(3)分别求得两种瓷砖的块数,然后代入数值求值即可;
(4)通过计算说明其瓷砖块数为偶数,从而得到答案.
(2)根据图形可以得出每一横行由(n+3)块瓷砖,每一竖列有(n+2)快瓷砖,第n个图形的白瓷砖的每行有(n+1)个,每列有n个,即可表示白瓷砖的数量,再让总数减去白瓷砖的数量即为黑瓷砖的数量;
(3)分别求得两种瓷砖的块数,然后代入数值求值即可;
(4)通过计算说明其瓷砖块数为偶数,从而得到答案.
解答:解:(1)22,20;
(2)(4n+6),n(n+1);
(3)当n=8时黑瓷砖有4×8+6=38(块),白瓷砖有8×9=72(块)
12×38+10×72=1176(元)(8分)
答:购买铺设第(8)个图形所需瓷砖的费用为1176元;
(4)不存在.
因为当n为正整数时,4n+6为偶数,n(n+1)为偶数,
所以(4n+6)﹢n(n+1)也为偶数,故所需瓷砖总数不可能为18325块.
(2)(4n+6),n(n+1);
(3)当n=8时黑瓷砖有4×8+6=38(块),白瓷砖有8×9=72(块)
12×38+10×72=1176(元)(8分)
答:购买铺设第(8)个图形所需瓷砖的费用为1176元;
(4)不存在.
因为当n为正整数时,4n+6为偶数,n(n+1)为偶数,
所以(4n+6)﹢n(n+1)也为偶数,故所需瓷砖总数不可能为18325块.
点评:本题考查规律型中的图形变化问题,解决此题的关键是能够正确结合图形用代数式表示出黑、白瓷砖的数量,再根据题意列方程求解.

练习册系列答案
相关题目