题目内容
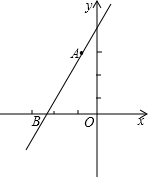 如图,直线y=kx+b经过点A(-1,3)与x轴交于点(-
如图,直线y=kx+b经过点A(-1,3)与x轴交于点(-| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
分析:由题意直线y=kx+b经过点A(-1,3)与x轴交于点(-
,0),根据待定系数法求出函数的解析式,然后再把直线解析式代入不等式组-
kx-
b≤0<x,再根据不等式的解法求出解集.
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:∵直线y=kx+b经过点A(-1,3)与x轴交于点(-
,0),
∴-k+b=3…①,-
k+b=0…②,
解方程①②得,k=
,b=
,
把k,b的值代入不等式组-
kx-
b≤0<x得:-
×
-
×
≤0,
∴
≤0恒成立,
∵x>0,
∴不等式的解集为:x>0,
故答案为x>0.
| 6 |
∴-k+b=3…①,-
| 6 |
解方程①②得,k=
3(
| ||
| 2 |
3
| ||
| 2 |
把k,b的值代入不等式组-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
3(
| ||
| 2 |
| 1 |
| 3 |
3
| ||
| 2 |
∴
-2
| ||
| 2 |
∵x>0,
∴不等式的解集为:x>0,
故答案为x>0.
点评:此题考查了一次函数的性质及用待定系数法求函数的解析式,把一次函数与不等式联系起来,还考查了一元一次不等式组解集的求法,利用不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解),来求出不等组的解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
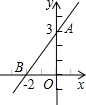 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
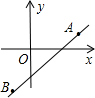 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
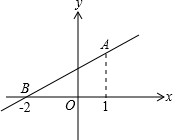 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为