题目内容
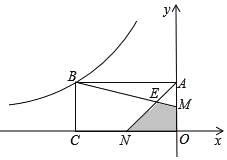
【题目】如图,E是边长为1的正方形ABCD的对角线BD上的一点,且BE=BA,P是CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R.则:(1)DE=__;(2)PQ+PR=__.
【答案】![]()
![]() ;
;
【解析】
(1)根据正方形的性质和勾股定理得出BD=![]() ,进而解答即可;
,进而解答即可;
(2)连接BP,过C作CM⊥BD,利用面积法求解,PQ+PR的值等于C点到BE的距离,即正方形对角线的一半.
(1)∵边长为1的正方形ABCD,
∴DB=![]() ,
,
∴DE=![]() 1;
1;
(2)连接BP,过C作CM⊥BD,如图所示:
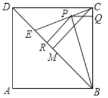
∵BC=BE,
∴S△BCE=S△BPE+S△BPC
=![]() BC×PQ+
BC×PQ+![]() BE×PR=
BE×PR=![]() BC×(PQ+PR)=
BC×(PQ+PR)=![]() BE×CM,
BE×CM,
∴PQ+PR=CM,
∵四边形ABCD是正方形,
∴∠BCD=![]() ,CD=BC=1,∠CBD=∠CDB=
,CD=BC=1,∠CBD=∠CDB=![]() ,
,
∴BD=![]() ,
,
∵BC=CD,CM⊥BD,
∴M为BD中点,
∴CM=![]() BD=
BD=![]() ,
,
即PQ+PR值是![]() .
.
故答案为:![]() ;
; ![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如图,用正方形是墩垒石梯,下图分别表示垒到一、二阶梯时的情况,那么照这样垒下去
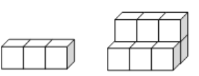
一级 二级
①填出下表中未填的两空,观察规律。
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 |
②到第n级阶梯时,共用正方体石墩_______________块(用n的代数式表示)