Question

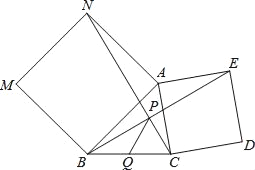
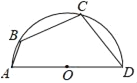
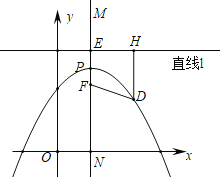
【题目】寻找神奇点！每条抛物线内都有一个神奇的点F（也叫焦点），还有一条与之配套的直线！（也叫准线），使得抛物线上的每个点到F的距离等于到直线l的距离．如图，对于抛物线上任意一点D，都有DF＝DH．

根据以上知识，我们来完成以下问题：

（1）因为抛物线是轴对称图形，由对称性可知这个神奇的点F应在抛物线的　 　上，且准线l一定与对称轴垂直即l⊥MN（对称轴）．

（2）若准线l与对称轴MN交于E，MN交抛物线于点P，则PE、PF的数量关系是PE　 　PF（填＞、＝、＜），

（3）求抛物线y＝﹣（x﹣2）2+4的神奇点（焦点）F的坐标．

Answer 1

【答案】（1）对称轴；（2）＝；（3）点F（2，）．

【解析】

（1）抛物线是轴对称图形，则点F应该在抛物线的对称轴上，即可求解；

（2）根据题意中焦点的性质解答即可；

（3）设PF＝c，则点F的坐标和直线l的解析式可用含c的代数式表示，设D（m，），然后根据两点间的距离公式分别表示出DF2和HD2，根据DF＝DH，可得关于m、c的方程，解方程即可求出c，进而可得结果．

解：（1）抛物线是轴对称图形，则点F应该在抛物线的对称轴上，

故答案为：对称轴；

（2）∵抛物线上的每个点到F的距离等于到直线l的距离，l⊥MN，∴PE=PF．

故答案为：＝；

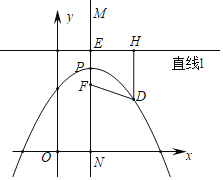
（3）如图，设PF＝c，顶点P（2，4），则点F（2，4﹣c），直线l：y＝c+4，

设D（m，），则DF2＝=，

HD2＝，

∵DF＝DH，∴=，

化简得：1﹣2c＝2c，解得：c＝，

故点F（2，）．