题目内容
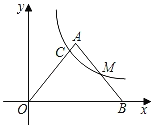
【题目】如图,点M是⊙O直径AB上一定点,点C是直径AB上一个动点,过点![]() 作
作![]() 交⊙O于点
交⊙O于点![]() ,作射线DM交⊙O于点N,连接BD.
,作射线DM交⊙O于点N,连接BD.

小勇根据学习函数的经验,对线段AC,BD,MN的长度之间的数量关系进行了探究.
下面是小勇的探究过程,请补充完整:
(1)对于点C在AB的不同位置,画图,测量,得到了线段AC,BD,MN的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AC/cm | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
BD/cm | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | 0.00 |
MN/cm | 4.00 | 3.27 | 2.83 | 2.53 | 2.31 | 2.14 | 2.00 |
在AC,BD,MN的长度这三个量中,如果选择________的长度为自变量,那么________的长度和________的长度为这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中确定的函数的图象;

(3)结合函数图象解决问题:当BD=MN时,线段AC的长度约为_____cm(结果精确到0.1).
【答案】(1)AC,BD,MN或BD,AC,MN;(2)见解析;(3)5.3
【解析】
(1)由函数的自变量及函数的定义即可得出答案
(2)利用描点法画出图象即可
(3)由数形结合的思想,直接观察图象,图1中BD=MN时,即为两图象相交时,此时的横坐标表示AC的长,大约为5.3厘米.
(1)由表格可确定BD和MN随着AC的变化而变化,AC和MN随着BD的变化而变化,故AC、BD的长度是自变量,BD或MN的长度和AC或MN的长度是自变量AC或BD的函数;
故答案为:AC,BD,MN或BD,AC,MN
(2)如图1或图2所示:
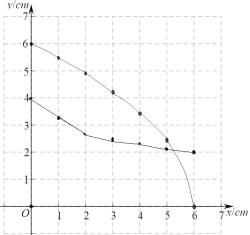
图1
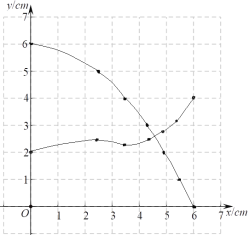
图2
(3)图1中BD=MN时,即为两图象相交时,此时的横坐标表示AC的长,大约为5.3厘米.
故答案为:5.3

【题目】人口数据又称为人口统计数据,是指国家和地区的相关人口管理部门通过户口登记、人口普査等方式统计得出的相关数据汇总.人口数据对国家和地区的人口状况、管理以及各项方针政策的制定都具有重要的意义.下面是关于人口数据的部分信息.
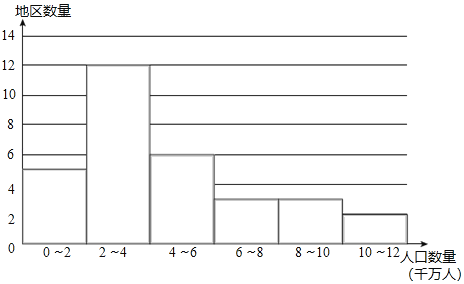
a.2018年中国大陆(不含港澳台)31个地区人口数量(单位:千万人)的频数分布直方图(数据分成6组:0≤x<2,2≤x<4,4≤x<6,6≤x<8,8≤x<10,10≤x≤12):
b.人口数量在2≤x<4这一组的是:
2.2 2.4 2.5 2.5 2.6 2.7 3.1 3.6 3.7 3.8 3.9 3.9
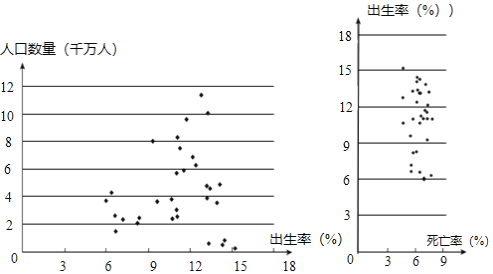
c.2018年中国大陆(不含港澳台)31个地区人口数量(单位:千万人)、出生率(单位:‰)、死亡率(单位:‰)的散点图:
d.如表是我国三次人口普查中年龄结构构成情况:
0~14岁人口比例 | 15~59岁人口比例 | 60岁以上人口比例 | |
第二次人口普查 | 40.4% | 54.1% | 5.5% |
第五次人口普查 | 22.89% | 66.78% | 10.33% |
第六次人口普查 | 16.6% | 70.14% | 13.26% |
e.世界各国的人口出生率差别很大,出生率可分为五等,最高>50‰,最低<20‰,2018年我国人口出生率降低至10.94‰,比2017年下降1.43个千分点.
根据以上信息,回答下列问题:
(1)2018年北京人口为2.2千万人,我国大陆(不含港澳台)地区中,人口数量从低到高排列,北京排在第 位.
(2)人口增长率=人口出生率﹣人口死亡率,我国大陆(不含港澳台)地区中人口在2018年出现负增长的地区有 个,在这些地区中,人口数量最少的地区人数为 千万人(保留小数点后一位).
(3)下列说法中合理的是 .
①我国人口基数较大,即使是人口出生率和增长率都缓慢增长的前提下,人口总数仍然是在不断攀升的,所以我国计划生育的基本国策是不变的;
②随着我国老龄化越来越严重,所以出台了“二孩政策”,目的是为了缓解老龄化的压力.
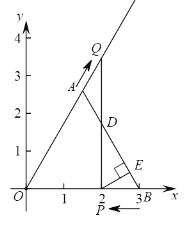
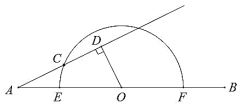
【题目】如图,点![]() 是线段
是线段![]() 的中点,
的中点,![]() 是以
是以![]() 为圆心,
为圆心,![]() 长为直径的半圆弧,点
长为直径的半圆弧,点![]() 是
是![]() 上一动点,过点
上一动点,过点![]() 作射线
作射线![]() 的垂线,垂足为
的垂线,垂足为![]() .已知
.已知![]() ,
,![]() ,设
,设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
小丽根据学习函数的经验,分别对函数![]() 和
和![]() 随自变量
随自变量![]() 变化而变化的规律进行了探究.下面是小丽的探究过程,请将它补充完整:
变化而变化的规律进行了探究.下面是小丽的探究过程,请将它补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到
的值进行取点、画图、测量,分别得到![]() 和
和![]() 与
与![]() 的几组对应值:
的几组对应值:
| 2 | 3 | 4 | 4.5 | 5 | 5.5 | 6 | 7 | 8 |
| 0 | 2.76 |
| 2.96 | 2.86 | 2.70 | 2.49 | 1.85 | 0 |
| 3.00 | 1.18 | 0 | 0.47 | 0.90 | 1.30 | 1.37 | 2.36 | 3.00 |
经测量,![]() 的值是______;(保留一位小数)
的值是______;(保留一位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() 和
和![]() ,并画出函数
,并画出函数![]() 、
、![]() 的图象;
的图象;
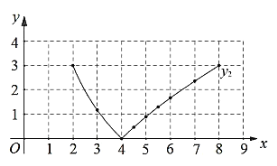
(3)结合函数图象,解决问题:连接![]() ,当
,当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长度约为______
的长度约为______![]() .(结果保留一位小数)
.(结果保留一位小数)
【题目】改革开放以来,人们的支付方式发生了巨大转变,近年来,移动支付已成为主要的支付方式之一,为了解某校学生上个月![]() 两种移动支付方式的使用情况,从全校
两种移动支付方式的使用情况,从全校![]() 名学生中随机抽取了
名学生中随机抽取了![]() 人,发现样本中
人,发现样本中![]() 两种支付方式都不使用的有
两种支付方式都不使用的有![]() 人,样本中仅使用
人,样本中仅使用![]() 种支付方式和仅使用
种支付方式和仅使用![]() 种支付方式的学生的支付金额
种支付方式的学生的支付金额![]() (元)的分布情况如下:
(元)的分布情况如下:
支付金额 支付方式 |
|
|
|
仅使用 |
|
|
|
仅使用 |
|
|
|
下面有四个推断:
①从样本中使用移动支付的学生中随机抽取一名学生,该生使用A支付方式的概率大于他使用B支付方式的概率;
②根据样本数据估计,全校1000名学生中.同时使用A、B两种支付方式的大约有400人;
③样本中仅使用A种支付方式的同学,上个月的支付金额的中位数一定不超过1000元;
④样本中仅使用B种支付方式的同学,上个月的支付金额的平均数一定不低于1000元.其中合理的是( )
A.①③B.②④C.①②③D.①②③④