题目内容
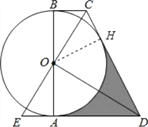
【题目】如图,AB为⊙O的直径,BC、AD是⊙O的切线,过O点作EC⊥OD,EC交BC于C,交直线AD于E.
(1)求证:CD是⊙O的切线;
(2)若AE=1,AD=3,求阴影部分的面积.

【答案】(1)见解析;(2) 3![]() ﹣π;
﹣π;
【解析】试题分析:(1)首先作OH⊥CD,垂足为H,由BC、AD是⊙O的切线,易证得△BOC≌△AOE(ASA),继而可得OD是CE的垂直平分线,则可判定DC=DE,即可得OD平分∠CDE,则可得OH=OA,证得CD是⊙O的切线;
(2)首先证得△AOE∽△ADO,然后由相似三角形的对应边成比例,求得OA的长,然后利用三角函数的性质,求得∠DOA的度数,继而求得答案.
试题解析:
(1)证明:作OH⊥CD,垂足为H,
∵BC、AD是⊙O的切线,
∴∠CBO=∠OAE=90°,
在△BOC和△AOE中,![]() ,
,
∴△BOC≌△AOE(ASA),
∴OC=OE,
又∵EC⊥OD,
∴DE=DC,
∴∠ODC=∠ODE,
∴OH=OA,
∴CD是⊙O的切线;
(2)∵∠E+∠AOE=90°,∠DOA+∠AOE=90°,
∴∠E=∠DOA,
又∵∠OAE=∠ODA=90°,
∴△AOE∽△ADO,
∴![]() =
=![]() ,
,
∴OA2=EAAD=1×3=3,
∵OA>0,
∴OA=![]() ,
,
∴tanE=![]() =
=![]() ,
,
∴∠DOA=∠E=60°,
∵DA=DH,∠OAD=∠OHD=90°,
∴∠DOH=∠DOA=60°,
∴S阴影部分=![]() ×3×
×3×![]() +
+![]() ×3×
×3×![]() ﹣
﹣![]() =3
=3![]() ﹣π.
﹣π.

【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数 | 54 | 45 | 30 | 24 | 21 | 12 |
人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.