题目内容
【题目】在一次数学课上，老师出示了这样一道题目：“如图，BD是矩形ABCD的对角线，将AB沿BE折叠，使A点落在BD上的点G处，将边CD沿DF折叠，使点C落在BD上的点H处，求证：四边形BEDF是平行四边形”．小丽选择了先证明△DEG≌△BFH，再证明DE=BF，进而得到四边形BEDF是平行四边形，小明向老师提出了另一种证明方法．
（1）小丽证明四边形BEDF是平行四边形的依据是；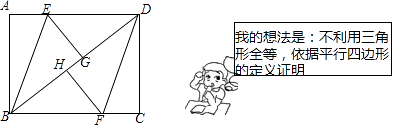
（2）按小明的想法写出证明过程；
（3）当学生们完成了证明后，老师又提出如下问题，连接EH，FG，若AB=6，BC=8，试求四边形EGFH的周长．
【答案】
（1）一组对边平行且相等的四边形是平行四边形
（2）证明：由翻折的性质可知：∠ABE=∠DBE═ 
，EG=EA，FH=FC
∠BDF═∠CDF= 
．
又∵四边形ABCD是矩形，
∴AD∥BC，AB∥CD，
∴∠ABD=∠CDB，
∴∠DBE=∠BDF，
∴BE∥DF，
又DE∥BF，
∴四边形BEDF是平行四边形（两组对边分别平行的四边形是平行四边形）；
（3）解：连接EH、GF，如图所示：
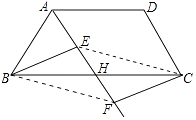
∵∠A=90°，AD=BC=8，AB=6，GB=AB=6，
∴BD= 
=10，
∴DG=BD﹣GB=4，
设AE=x，则DE=8﹣x，EG=AE=x，
在Rt△DGE中，由勾股定理得（8﹣x）2=x2+42，
解得x=3，
∴AE=3，
同理FH=3，
由（1）得：EG=FH，
∵EG⊥BD，FH⊥BD，
∴EG∥FH，
∴四边形EGFH是平行四边形，EG=FH=3，
∵BG=DH=6，
∴DG=BH=4，
∴GH=2，
在Rt△EGH中， 
，
四边形EGFH的周长为 
．
【解析】（1）解：一组对边平行且相等的四边形是平行四边形；理由如下：
∵四边形ABCD是矩形，
∴AD∥BC，AD=BC，AB∥CD，∠A=∠C=90°，
∴∠EDG=∠FBH，
由折叠的性质得：∠EGB=∠A=90°，GB=AB，HD=CD，
∴∠DGE=∠BHF=90°，DG=BH，
在△DEG和△BFH中，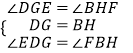 
，
∴△DEG≌△BFH（ASA），
∴DE=BF，
又∵DE∥BF，
∴四边形BEDF是平行四边形；
所以答案是：一组对边平行且相等的四边形是平行四边形；
【考点精析】根据题目的已知条件，利用平行四边形的判定与性质的相关知识可以得到问题的答案，需要掌握若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．
