题目内容
【题目】如图，一次函数y=-
x+b的图象与x轴、y轴分别交于点A、B，线段AB的中点为D（3，2）．将△AOB沿直线CD折叠，使点A与点B重合，直线CD与x轴交于点C．
（1）求此一次函数的解析式；
（2）求点C的坐标；
（3）在坐标平面内存在点P（除点C外），使得以A、D、P为顶点的三角形与△ACD全等，请直接写出点P的坐标．
【答案】（1）一次函数解析式为y=-
x+4.（2）C（
，0）；（3）P1（
，4）；P2（
，-2）；P3（
，2）．
【解析】
试题分析：（1）根据线段中点的性质，可得B点，A点坐标，根据待定系数法，可得函数解析式；
（2）OC=x，根据翻折变换的性质用x表示出BC的长，再根据勾股定理求解即可；
（3）当△ACD≌△AP1D时，根据C、P点关于D点对称，可得P点坐标，当△ACD≌△DP2A时，根据全等三角形的判定与性质，可得答案；当△ACD≌△DP3A时，根据线段中点的性质，可得答案．
试题解析：（1）设A点坐标为（a，0），B点坐标为（0，b），
由线段AB的中点为D（3，2），得
=3，
=2，
解得a=6，b=4．
即A（6，0），B（0，4）
故一次函数解析式为y=-x+4.
（2）如图1：
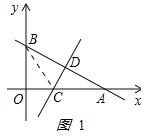
连接BC，设OC=x，则AC=CB=6-x，
∵∠BOA=90°，
∴OB2+OC2=CB2，
42+x2=（6-x）2，
解得x=，
即C（，0）；
（3）①当△ACD≌△APD时，设P1（c，d），
由D是PC的中点，得
，
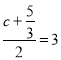=2，
解得c=，d=4，
即P1（，4）；
如图2：
，
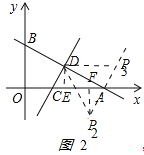②当△ACD≌△DP2A时，
做DE⊥AC与E，P2F⊥AC与F点，DE=2，CE=
，
由△CDE≌△AP2F，
AF=CE=
，P2F=DE=2，
OF=6-=，
∴P2（，-2）；
③当△ACD≌△DP3A时，设P3（e，f）
A是线段P2P3的中点，得
，
，
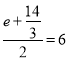解得e=，f=2，
即P3（，2），
综上所述：P1（，4）；P2（，-2）；P3（，2）．
