题目内容
【题目】如图,点A,B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.
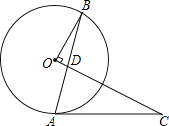
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OC=13,OD=1,求⊙O的半径及tanB.
【答案】(1)AC是⊙O的切线;见解析(2)![]() .
.
【解析】
试题分析:(1)根据已知条件“∠CAD=∠CDA”、对顶角∠BDO=∠CDA可以推知∠BDO=∠CAD;然后根据等腰三角形OAB的两个底角相等、直角三角形的两个锐角互余的性质推知∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°,可得AC是⊙O的切线.
(2)由勾股定理求出OA,得出OB,由三角函数的定义求出tanB即可.
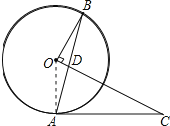
(1)证明:连接OA,如图所示:
∵AC=CD,
∴∠CAD=∠CDA,
∵∠BDO=∠CDA,
∴∠BDO=∠CAD,
又∵OA=OB,
∴∠B=∠OAB,
∵OB⊥OC,
∴∠B+∠BDO=∠OAB+∠CAD=90°,
即∠OAC=90°,
∴AC是⊙O的切线;
(2)解:∵OC=13,OD=1,
∴AC=CD=OC﹣OD=12,
∴OA=![]() =
=![]() =5,
=5,
即⊙O的半径为5,
∵OB=OA=5,
∴tanB=![]() =
=![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目