题目内容
【题目】如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
则∠A=∠F,请说明理由.
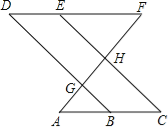
解:∵∠AGB=∠EHF
∠AGB= (对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC
∴∠ =∠DBA ( 两直线平行,同位角相等)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F .
【答案】已知;∠DGF;同位角相等,两直线平行;C;AC;两直线平行,内错角相等
【解析】试题分析:根据对顶角相等推出同位角∠EHF=∠DGF,从而证得两直线DB∥EC;然后由平行线的性质知内错角∠DBA=∠D,即可根据平行线的判定定理得两直线DF∥AC,最后由平行线的性质证得:∠A=∠F.
试题解析:∵∠AGB=∠EHF(已知),∠AGB=∠DGF(对顶角相等),
∴∠EHF=∠DGF
∴DB∥EC(同位角相等,两直线平行),
∴∠C="∠DBA" ( 两直线平行,同位角相等);
又∵∠C=∠D(已知),
∴∠DBA=∠D(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等);

练习册系列答案
相关题目