题目内容
【题目】如图,已知圆O是△ABC的外接圆,AB是圆O的直径,C是圆上的一点,D是AB延长线上的一点,AE⊥CD交DC的延长线于点E,且AC平分∠EAB.
(1)求证:DE是圆O的切线.
(2)若AB=6,AE=4.8,求BD和BC的长.

【答案】(1)见解析;(2)2,![]()
【解析】分析:(1)要证DE是![]() 的切线,只要连接OC,再证
的切线,只要连接OC,再证![]() 即可.
即可.
(2)已知两边长,求其它边的长,可以来三角形相似,对应边成比例来求.
详解:(1)证明:连接OC;
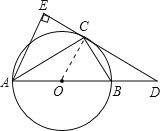
∵AC平分∠EAB,
∴∠EAC=∠BAC;
又在圆中OA=OC,
∴∠ACO=∠BAC,
∴∠EAC=∠ACO,
∴OC∥AE(内错角相等,两直线平行);
则由AE⊥DC知OC⊥DC,
即DE是![]() 的切线.
的切线.
(2)∵![]()
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴BD=2;
∵Rt![]() ∽Rt
∽Rt![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AC2=![]() ,
,
由勾股定理得:BC=![]() .
.

练习册系列答案
相关题目
【题目】为鼓励居民节约用电,国家发改委发布文件在全国实行“阶梯电价”收费,重庆结合本市实际,根据国家发改委文件要求,决定从2016年1月1日起对居民生活用电实行“阶梯电价”收费,具体收费标准见下表.若2016年8月份,该市居民甲生活用电240千瓦时(能量量度单位,1千瓦时即1度),交电费130元.
一户居民一个月用电量 | 电费价格(元/千瓦时) | |
第一档 | 不超过200千瓦时 | 0.52 |
第二档 | 超过200千瓦时但不超过320千瓦时 |
|
第三档 | 超过320千瓦时 | 0.95 |
(1)求上表中的![]() 的值;
的值;
(2)若该市居民乙某月交电费220元,居民乙当月的生活用电量为多少千瓦时?
(3)实行“阶梯电价”收费后,该市居民丙月用电量为多少千瓦时,其当月的平均电价为0.55元/千瓦时?




