题目内容
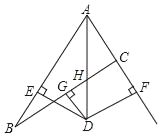
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P.Q分別是AB、AC上的动点,且满足BP=AQ,D是BC的中点,当点P运动到___时,四边形APDQ是正方形.

【答案】AB的中点.
【解析】
若四边形APDQ是正方形,则DP⊥AP,得到P点是AB的中点.
当P点运动到AB的中点时,四边形APDQ是正方形;理由如下:
∵∠BAC=90°,AB=AC,D为BC中点,
∴AD⊥BC,AD=BD=DC,∠B=∠C=45°,
∴△ABD是等腰直角三角形,
当P为AB的中点时,DP⊥AB,即∠APD=90°,
又∵∠A=90°,∠PDQ=90°,
∴四边形APDQ为矩形,
又∵DP=AP=![]() AB,
AB,
∴矩形APDQ为正方形,
故答案为:AB的中点.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
【题目】某冷库一天的冷冻食品进出记录如下表![]() 运进用正数表示,运出用负数表示
运进用正数表示,运出用负数表示![]() :
:
进出数量 |
| 4 |
| 2 |
|
进出次数 | 2 | 1 | 3 | 3 | 2 |
(1)这天冷库的冷冻食品比原来增加了还是减少了?请说明理由.
(2)根据实际情况,现有两种方案:
方案一:运进每吨冷冻食品费用500元,运出每吨冷冻食品费用800元.
方案二:不管运进还是运出每吨冷冻食品费用都是600元.从节约运费的角度考虑,选用哪一种方案比较合适?