题目内容
【题目】已知,直线![]() 与反比例函数
与反比例函数![]() 交于点
交于点![]() ,且点
,且点![]() 的横坐标为4,过
的横坐标为4,过![]() 轴上一点
轴上一点![]() 作
作![]() 垂直于
垂直于![]() 交
交![]() 于
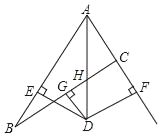
于![]() 点,如图.
点,如图.

(1)若点![]() 是线段
是线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() ,
,![]() ,垂足分别于
,垂足分别于![]() 、
、![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
(2)在(1)的![]() 取得最小值的前提下,将
取得最小值的前提下,将![]() 沿射线
沿射线![]() 平移,记平移后的三角形为
平移,记平移后的三角形为![]() ,当
,当![]() 时,在平面内存在点
时,在平面内存在点![]() ,使得
,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点构成平行四边形,这样的点
四点构成平行四边形,这样的点![]() 有几个?直接写出点
有几个?直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() 最小值为4.8;(2)这样的
最小值为4.8;(2)这样的![]() 点有3个,
点有3个,![]() ;
;![]() ;
;![]() .
.
【解析】
(1)利用反比例函数图象上点的坐标特征可求出点A的坐标,由点A的坐标,利用待定系数法可求出直线0A的解析式,设点P的坐标为(m,![]() m)(
m)(![]() ),则PE=
),则PE=![]() m,PF=8-m,利用勾股定理可找出EF2关于m的函数关系式,再利用二次函数的性质,即可求出EF2的最小值,进而可得出段EF长度的最小值;
m,PF=8-m,利用勾股定理可找出EF2关于m的函数关系式,再利用二次函数的性质,即可求出EF2的最小值,进而可得出段EF长度的最小值;
(2)由(1)的结论结合平移的性质,可得出平移后点![]() 、
、![]() 、
、![]() 的坐标.
的坐标.
解:(1)当x=4时,![]()
∴![]()
设直线OA的解析式为![]()
将![]() 代入
代入![]() 得k=
得k=![]()
设点P的坐标为(m,![]() m)(
m)(![]() ) 则PE=
) 则PE=![]() m,PF=8-m
m,PF=8-m
∴FE2=PF2+PE2即FE2=(![]() m)2+(8-m)2=
m)2+(8-m)2=![]() (m-
(m-![]() )2+
)2+![]()
![]()
∴当m=![]() 时,EF2取得最小值,此时EF最小值为
时,EF2取得最小值,此时EF最小值为![]()
∴![]() 最小值为4.8.
最小值为4.8.
(2)这样的![]() 点有3个.
点有3个.
![]() ;
;![]() ;
;![]()

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目