题目内容
 如图,CD是Rt△ABC的斜边AB上的高线,∠BAC的平分线分别交BC,CD于点E,F,
如图,CD是Rt△ABC的斜边AB上的高线,∠BAC的平分线分别交BC,CD于点E,F,
求证:(1)△ACF∽△ABE;
(2)AC•AE=AF•AB.
证明:(1)∵CD是Rt△ABC斜边上的高线,
∴∠ACF=90°-∠BAC=∠B;
∵AE平分∠BAC,
∴∠CAF=∠BAE,
∴△ACF∽△ABE.
(2)∵△ACF∽△ABE,
∴ ,
,
∴AC•AE=AF•AB.
分析:(1)由于EA平分∠CAB,则∠CAE=∠BAE,在Rt△ABC中,CD⊥AB,根据同角的余角相等可证得∠ACF=∠B,由此可判定所求的两个三角形相似.
(2)根据(1)的相似三角形所得比例线段即可得证.
点评:此题主要考查的是相似三角形的判定和性质,属于基础知识,难度不大.
∴∠ACF=90°-∠BAC=∠B;
∵AE平分∠BAC,
∴∠CAF=∠BAE,
∴△ACF∽△ABE.
(2)∵△ACF∽△ABE,
∴
 ,
,∴AC•AE=AF•AB.
分析:(1)由于EA平分∠CAB,则∠CAE=∠BAE,在Rt△ABC中,CD⊥AB,根据同角的余角相等可证得∠ACF=∠B,由此可判定所求的两个三角形相似.
(2)根据(1)的相似三角形所得比例线段即可得证.
点评:此题主要考查的是相似三角形的判定和性质,属于基础知识,难度不大.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
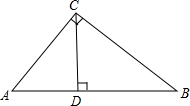 如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )
如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( ) 18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于
18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于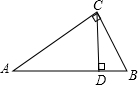 如图,CD是Rt△ABC斜边上的高线,若sinA=
如图,CD是Rt△ABC斜边上的高线,若sinA=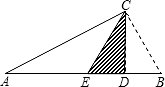 如图,CD是Rt△ABC斜边AB上的高,直角边AC=
如图,CD是Rt△ABC斜边AB上的高,直角边AC=