题目内容
如图，正方形ABCD中，E、F分别为AB、BC的中点，AF与DE相交于点O，则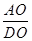
为 （ ）
A．
B．
C．
D．
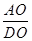为 （ ）A．
B．
C．
D．
D
试题分析：先根据正方形的性质结合E、F分别为AB、BC的中点证得△ADE≌△BAF，再结合同角的余角相等即可证得△AOD∽△EAD，根据相似三角形的性质即可证得结论.
∵正方形ABCD，E、F分别为AB、BC的中点
∴AE=BF，AD=AB，∠EAD=∠B=90°
∴△ADE≌△BAF
∴∠ADE=∠BAF，∠AED=∠BFA
∵∠DAO+∠FAB=90°，∠FAB+∠BFA=90°
∴∠DAO=∠BFA，
∴∠DAO=∠AED
∴△AOD∽△EAD
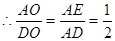
故选D．
点评：解答本题的关键是熟练掌握相似三角形的性质：相似三角形的对应边成比例；同时注意对应字母写在对应位置上.
练习册系列答案
相关题目
，那么下列式子中一定成立的是（ ） 
＝
．
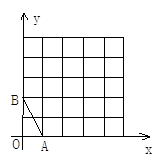
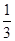，求
，如果
=
，那么
= ．