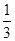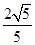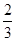题目内容
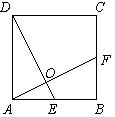
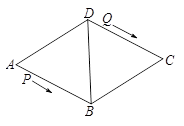
如图,在正△ABC中,点D是AC的中点,点E在BC上,且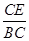 =
=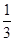 .
.
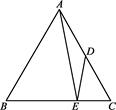
求证:(1)△ABE∽△DCE;
(2)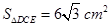 ,求
,求
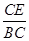 =
=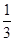 .
.
求证:(1)△ABE∽△DCE;
(2)
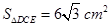 ,求
,求
(1)∵ΔABC是正三角形
∴∠B=∠C,AB=AC
∵点D是AC的中点
∴AC=2CD
∵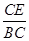 =
=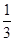
∴BE=2CE
∴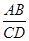 =
=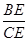
∵∠B=∠C
∴ΔABE∽ΔDCE;
(2)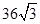
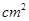
∴∠B=∠C,AB=AC
∵点D是AC的中点
∴AC=2CD
∵
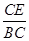 =
=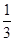
∴BE=2CE
∴
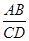 =
=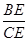
∵∠B=∠C
∴ΔABE∽ΔDCE;
(2)
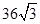
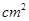
试题分析:(1)由ΔABC是正三角形可得∠B=∠C,AB=AC,再结合点D是AC的中点,
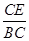 =
=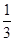 ,即可证得结论;
,即可证得结论;(2)由(1)知△ABE∽△DCE,由相似三角形的性质可得△ABE的面积,即可求得△AED与△EDC的面积,从而得到结果.
(1)∵ΔABC是正三角形
∴∠B=∠C,AB=AC
∵点D是AC的中点
∴AC=2CD
∵
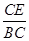 =
=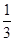
∴BE=2CE
∵∠B=∠C
∴
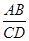 =
=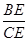
∴ΔABE∽ΔDCE;
(2)∵△ABE∽△DCE
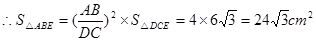
又∵AD=DC且△AED与△EDC具有相同的高和底
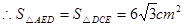
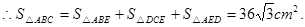
点评:解答本题的关键是已知其中一个三角形的面积,根据两个相似三角形的面积之比等于边之比的平方,求出另一个三角形的面积,另外熟记同底同高的三角形的面积相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =
=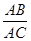 ; (B)
; (B) =
=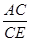 ;
; =
=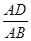 ; (D)
; (D) .
.
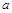 cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF与问题(2)中的△AMN相似,试求
cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF与问题(2)中的△AMN相似,试求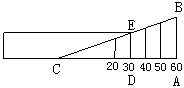
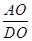 为 ( )
为 ( )