题目内容
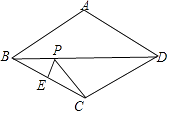
【题目】已知,在ABCD中,连结对角线AC,∠CAD平分线AF交CD于点F,∠ACD平分线CG交AD于点G,AF,CG交于点O,点E为BC上一点,且∠BAE=∠GCD.
(1)如图1,若△ACD是等边三角形,OC=2,求ABCD的面积;
(2)如图2,若△ACD是等腰直角三角形,∠CAD=90°,求证:CE+2OF=AC.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据平行四边形ABCD的面积=2S△ACD,求出△ACD的面积即可.
(2)如图2中,延长OF到M,使得FM=OF,连接CM.只要证明AC=AM,OA=AG=CE即可解决问题.
解:(1)∵△ACD是等边三角形,∴AC=CD=AD,
∠ACD=∠D=∠CAD=60°,∵∠OAC=∠OCA=30°,
∴OA=OC=2,∵CG平分∠ACD,∴CG⊥AD,
在Rt∠AOG中,∵∠OAG=30°,OA=2,∴OG=![]() OA=1,
OA=1,
AG=![]() ,∴AD=2AG=2
,∴AD=2AG=2![]() ,∴S△ACD=
,∴S△ACD=![]() AD·CG=3
AD·CG=3![]() .
.
∴平行四边形ABCD的面积=2·S△ACD=6![]()
(2)延长OF到M,使得FM=OF,连结CM.
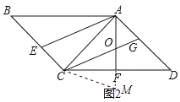
∵△ACD是等腰直角三角形,AF,CG是角平分线,∴AF⊥CF,
∠OAC=∠D=∠ACD=45°,∠OCA=∠DCG=22.5°,
∴∠COF=∠OAC+∠OCA=67.5°,∠AGC=∠D+∠GCD=67.5°,
∴∠AOG=∠AGO,∴OA=AG,∵CF⊥OM,OF=FM,∴CO=CM,
∴∠M=∠COM=67.5°,∴∠ACM=180°-∠CAM-∠M=67.5°,
∴∠ACM=∠M,∴CA=AM,∵∠BAE=∠GCD=22.5°,AB∥CD,
∴∠BAC=∠ACD=45°,∴∠EAC=∠ACG=22.5°,∴AE∥CG,
∵EC∥AG,∴四边形AECG是平行四边形,∴CE=AG=OA,
∴AC=AM=OA+OM=CE+2OF

【题目】小李在某商场购买![]() 两种商品若干次(每次
两种商品若干次(每次![]() 商品都买) ,其中前两次均按标价购买,第三次购买时,
商品都买) ,其中前两次均按标价购买,第三次购买时,![]() 商品同时打折.三次购买
商品同时打折.三次购买![]() 商品的数量和费用如下表所示:
商品的数量和费用如下表所示:
购买A商品的数量/个 | 购买B商品的数量/个 | 购买总费用/元 | |
第一次 |
|
|
|
第二次 |
|
|
|
第三次 |
|
|
|
(1)求![]() 商品的标价各是多少元?
商品的标价各是多少元?
(2)若小李第三次购买时![]() 商品的折扣相同,则商场是打几折出售这两种商品的?
商品的折扣相同,则商场是打几折出售这两种商品的?
(3)在(2)的条件下,若小李第四次购买![]() 商品共花去了
商品共花去了![]() 元,则小李的购买方案可能有哪几种?
元,则小李的购买方案可能有哪几种?