题目内容
如图,已知△ABC是边长为4的等边三角形,AB在x轴上,点C在第一象限,AC交y轴于点D,点A的坐标为(-1,0).
(1)求B、C、D三点的坐标;
(2)抛物线y=ax2+bx+c经过B、C、D三点,求它的解析式;
(3)过点D作DE∥AB交经过B、C、D三点的抛物线于点E,求DE的长.
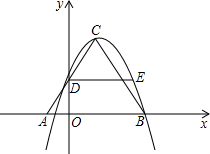
(1)求B、C、D三点的坐标;
(2)抛物线y=ax2+bx+c经过B、C、D三点,求它的解析式;
(3)过点D作DE∥AB交经过B、C、D三点的抛物线于点E,求DE的长.

(1)OB=AB-OA=4-1=3,则B的坐标是(3,0);
C点的横坐标是:
(-1+3)=1,三角形的高是:4×
=2
,
则C的坐标是:(1,2
);
设直线AC的解析式是:y=kx+b,根据题意得:
,
解得:
,
则直线的解析式是:y=
x+
,
令x=0,解得:y=
,
则D的坐标是:(0,
);
(2)根据题意得:
,
解得:
,
则函数的解析式是:y=-
x2+
x+
;
(3)在:y=-
x2+
x+
中,令y=
,
得到-
x2+
x+
=
,
解得:x=0或
.
故DE=
.
C点的横坐标是:
| 1 |
| 2 |
| ||
| 2 |
| 3 |
则C的坐标是:(1,2
| 3 |
设直线AC的解析式是:y=kx+b,根据题意得:
|
解得:
|
则直线的解析式是:y=
| 3 |
| 3 |
令x=0,解得:y=
| 3 |
则D的坐标是:(0,
| 3 |
(2)根据题意得:
|
解得:
|
则函数的解析式是:y=-
2
| ||
| 3 |
5
| ||
| 3 |
| 3 |
(3)在:y=-
2
| ||
| 3 |
5
| ||
| 3 |
| 3 |
| 3 |
得到-
2
| ||
| 3 |
5
| ||
| 3 |
| 3 |
| 3 |
解得:x=0或
| 5 |
| 2 |
故DE=
| 5 |
| 2 |

练习册系列答案
相关题目

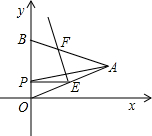 OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE
OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE

 的矩形花圃.
的矩形花圃.