题目内容
【题目】已知抛物线
与x轴最多有一个交点.现有以下四个结论：①
；②该抛物线的对称轴在y轴的左侧；③关于x的方程
有实数根；④
.其中正确结论的个数为（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】A
【解析】
根据抛物线的系数与图象的关系即可求出答案．
∵抛物线
与x轴最多有一个交点.
∴△=b2-4ac≤0，即b2≤4ac，故①错误；
①∵a＞b＞0，
∴
<1，
∴
>
，
∴对称轴位于y轴的左侧，故②错误；
由题意可知：对于任意的x，都有y=ax2+bx+c≥0，
∴ax2+bx+c+1≥1＞0，即该方程无解，故③错误；
由于抛物线与x轴最多只有一个交点，a＞0，
∴对于任意的x，y≥0，
令x=-1，
∴a-b+c≥0，故④正确
故选A.
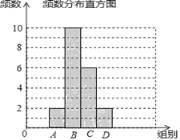
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理，绘制了如下不完整的统计图表：
组别 | 步数分组 | 频率 |
A | x＜6000 | 0.1 |
B | 6000≤x＜7000 | 0.5 |
C | 7000≤x＜8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题：
（1）填空：m＝ ，n＝ ；并补全条形统计图；
（2）这20名朋友一天行走步数的中位数落在 组；（填组别）
（3）张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞，请求出甲、乙被同时点赞的概率．
【题目】某超市为了销售一种新型“吸水拖把”，对销售情况作了调查，结果发现每月销售量y（只）与销售单价x（元）满足一次函数关系，所调查的部分数据如表：（已知每只进价为10元，销售单价为整数，每只利润＝销售单价﹣进价）
销售单价x（元） | 20 | 22 | 25 | … |
月销售额y（只） | 300 | 280 | 250 | … |
（1）求出y与x之间的函数表达式
（2）该新型“吸水拖把”每月的总利润为w（元），求w关于x的函数表达式，并指出销售单价为多少元时利润最大，最大利润是多少元？
（3）由于该新型“吸水拖把”市场需求量较大，厂家又进行了改装，此时超市老板发现进价提高了m元，当每月销售量与销售单价仍满足上述一次函数关系，随着销量的增大，最大利润能减少1750元，求m的值．
