题目内容
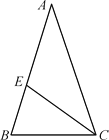
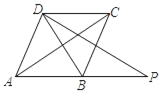
【题目】如图，B是线段AP的中点，以AB为边构造菱形ABCD，连接PD．若tan∠BDP＝
，AB＝13，则BD的长为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
证明△CED∽△AEP，根据相似三角形对应边成比例得：
=
，设CE＝x，得AE＝2x，由三角函数得tan∠BDP＝tan∠ODE＝
=
，得OD＝x＝OB，由勾股定理列方程可得结论．
解：如图，
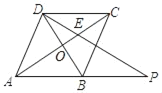
∵四边形ABCD是菱形，
∴CD∥AP，AC⊥BD，CD＝AB，
∴△CED∽△AEP，
∴=，
设CE＝x，
∵B是AP的中点，
∴AP＝2AB＝2CD，
∴=，
∴AE＝2x，
∴AC＝3x，
∴AO＝OC＝
x，
∴OE＝x﹣x＝x，
∵AC⊥BD，
∴∠DOE＝90°，
tan∠BDP＝tan∠ODE＝=，
∴OD＝x＝OB，
Rt△AOB中，由勾股定理得：AB2＝AO2+OB2，
132＝x2+（x）2，
x＝2
，
∴BD＝4．
故选：D．
练习册系列答案
相关题目
【题目】某超市为了销售一种新型“吸水拖把”，对销售情况作了调查，结果发现每月销售量y（只）与销售单价x（元）满足一次函数关系，所调查的部分数据如表：（已知每只进价为10元，销售单价为整数，每只利润＝销售单价﹣进价）
销售单价x（元） | 20 | 22 | 25 | … |
月销售额y（只） | 300 | 280 | 250 | … |
（1）求出y与x之间的函数表达式
（2）该新型“吸水拖把”每月的总利润为w（元），求w关于x的函数表达式，并指出销售单价为多少元时利润最大，最大利润是多少元？
（3）由于该新型“吸水拖把”市场需求量较大，厂家又进行了改装，此时超市老板发现进价提高了m元，当每月销售量与销售单价仍满足上述一次函数关系，随着销量的增大，最大利润能减少1750元，求m的值．
