题目内容
【题目】在![]() 中,
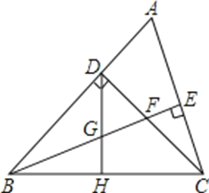
中,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,
,![]() 交于点
交于点![]() ,若
,若![]() ,则四边形
,则四边形![]() 的面积为________。
的面积为________。
【答案】![]()
【解析】
连接DE,根据相似三角形的判定定理得出△DCE∽△ABC,进而判断出AB∥CD、△DEF∽△ABF,再根据相似三角形的性质即可进行解答.
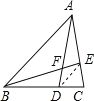 连接DE,
连接DE,
∵AE=2CE,BD=2CD,
∴![]() =
=![]() ,且夹角∠C为公共角,
,且夹角∠C为公共角,
∴△DCE∽△ABC,
∴∠CED=∠CAB,
∴AB∥DE,
∴△CDE∽△CBA,
∴![]() =
=![]() =
= ![]() ,
,
∴![]() =
= ![]() ,
,
∵S△ABC=3,
∴S△CDE=3×![]() =
=![]() ,
,
且∠EDA=∠BAD,∠BED=∠ABE,
∴△DEF∽△ABF,
∴![]() =
=![]() =
=![]() ,
,
∴设S△DEF=x,则S△AEF=S△BDF=3x,S△ABF=9x,
∴x+3x+3x+9x=3![]() ,
,
解得:x=![]() ,
,
∴S△DEF=![]() ,
,
∴S△DEF+S△CDE=![]() +
+![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目