题目内容
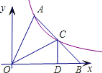
【题目】如图,已知![]() ,
,![]() 是一次函数
是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
![]() 求直线
求直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标及
的坐标及![]() 的面积;
的面积;
![]() 在
在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的值最大?若存在,直接写出点
的值最大?若存在,直接写出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
![]() 当点
当点![]() 在双曲线上运动时,作以
在双曲线上运动时,作以![]() 、
、![]() 为邻边的平行四边形,求平行四边形周长最小时点
为邻边的平行四边形,求平行四边形周长最小时点![]() 的坐标.
的坐标.

【答案】![]() ;
;![]() 存在,
存在, ![]()
![]() 或
或![]() .
.
【解析】
(1)利用xy=m求出反比例函数解析式,进而利用待定系数法求一次函数解析式,再求出图象与x轴交点坐标,进而得出三角形面积;
(2)作B点关于x轴对称点B′,连接AB′,直线AB′与x轴交点即为P点,此时PBPA最大,进而利用待定系数法求一次函数解析式求出图象与x轴交点坐标即可;
(3)利用当横纵坐标的绝对值相等时OQ长度最短,平行四边形周长最小,进而求出即可.
![]() ∵
∵![]() ,
,![]() 是一次函数
是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点,
的图象的两个交点,
∴![]() ,
,
∴反比例函数![]() ,
,
∴![]() ,
,
解得:![]() ,
,
将![]() ,
,![]() 代入一次函数
代入一次函数![]() ,
,
得:![]() ,
,
解得:![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
当![]() 时,
时,![]() ,
,
∴直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标为:
的坐标为:![]() ,
,
∴![]() ;
;
![]() 存在,作
存在,作![]() 点关于
点关于![]() 轴对称点
轴对称点![]() ,连接
,连接![]() ,直线
,直线![]() 与
与![]() 轴交点即为
轴交点即为![]() 点,此时
点,此时![]() 最大.
最大.
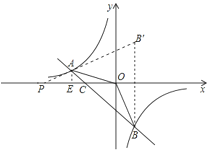
∵![]() ,∴
,∴![]() ,
,
将![]() ,
,![]() 代入
代入![]() 得:
得:
![]() ,
,
解得: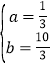 ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ;
;
![]() 作以
作以![]() 、
、![]() 为邻边的平行四边形,当横纵坐标的绝对值相等时
为邻边的平行四边形,当横纵坐标的绝对值相等时![]() 长度最短,平行四边形周长最小,
长度最短,平行四边形周长最小,
∴![]() ,
,
解得:![]() ,
,
∴![]()
![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目