题目内容
【题目】已知⊙O的半径为12cm,弦AB=12![]() cm.
cm.
(1)求圆心O到弦AB的距离.
(2)若弦AB恰好是△OCD的中位线,以CD中点E为圆点,R为半径作⊙E,当⊙O和⊙E相切时,求R的值.
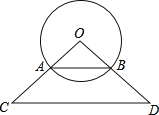
【答案】(1) ![]() cm;(2) 分为两种情况:当两圆外切时,半径
cm;(2) 分为两种情况:当两圆外切时,半径![]() cm,当两圆内切时,半径
cm,当两圆内切时,半径![]() cm.
cm.
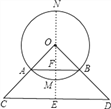
【解析】分析:(1)过O作OF⊥AB于F,交CD于E,根据等腰三角形性质求出AF,根据勾股定理求出OF即可;
(2)求出OE,求出EM和EN,即可得出答案.
本题解析::(1)过O作OF⊥AB于F,交CD于E,
∵OA=OB,
∴AF=BF=![]() AB=
AB=![]() ×12
×12![]() cm=6
cm=6![]() cm,
cm,
在Rt△OAF中,由勾股定理得:OF=![]() (cm),
(cm),
即圆心O到弦AB的距离是6![]() cm;
cm;
(2)∵OF=AF=6![]() cm,
cm,
∴∠OAB=45°,
∵AB是△OCD的中位线,
∴CD=2AB=24![]() cm,
cm,
∴OF=EF=6![]() cm,
cm,
即ME=OE-0M=6![]() +6
+6![]() -12=(12
-12=(12![]() -12)cm,
-12)cm,
分为两种情况:当两圆外切时,半径R=ME=(12![]() -12)cm,
-12)cm,
当两圆内切时,半径R=EN=(12![]() +12)cm.
+12)cm.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目