题目内容
【题目】在
中，AH是BC边上的高，若CH- BH= AB，
，则∠BAC= ______。
【答案】75°或35°
【解析】
当∠ABC为锐角时，过点A作AD=AB，交BC于点D，则可得出∠ADB=∠ABH=70°，BH=DH，结合AB+BH=CH、CH=CD+DH，可得出CD=AB=AD，进而求出∠C的度数，再求出∠BAC的度数；当∠ABC为钝角时，由AB+BH=CH可得出AB=BC，利用等腰三角形的性质及三角形外角的性质即可求出∠BAC的度数．综上即可得出结论．
解：当∠ABC为锐角时，过点A作AD=AB，交BC于点D，如图1所示．
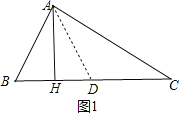
∵AB=AD，
∴∠ADB=∠ABH=70°，BH=DH．
∵AB+BH=CH，CH=CD+DH，
∴CD=AB=AD，
∴∠C=
∠ADB=35°，
∴∠BAC=180°-∠ABH-∠C=75°．
当∠ABC为钝角时，如图2所示．
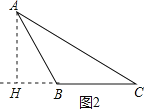
∵AB+BH=CH，
∴AB=BC，
∴∠BAC=∠ACB=∠ABH=35°．
故答案为：75°或35°．
练习册系列答案
阅读快车系列答案
相关题目
