题目内容
【题目】如图,直角三角形ABC与直角三角形BDE中,点B,C,D在同一条直线上,已知AC=AE=CD,∠BAC和∠ACB的角平分线交于点F,连DF,EF,分别交AB、BC于M、N,已知点F到△ABC三边距离为3,则△BMN的周长为____________.
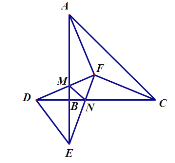
【答案】6
【解析】
由角平分线和三角形的内角和定理可得∠AFC=135°,由△AFC≌△DFC可得∠DFC=∠AFC=135°,可得∠AFD=90°.同理可得∠CFE=90°,可求得∠MFN=45°,过点F作FP⊥AB于点P,FQ⊥BC于点Q,由正方形的半角模型可得MN=MP+NQ,由此即可得出答案.
解:过点F作FP⊥AB于点P,FQ⊥BC于点Q,过点F作FG⊥FM,交BC于点G.
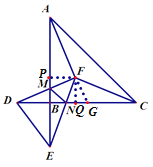
∵点F是∠BAC和∠BCA的角平分线交点,
∴FP=FQ=3,
∵∠ABC=90°,
∴四边形BPFQ是正方形,
∴BP=BQ=3.
在Rt△ABC中,∠BAC+∠BCA=90°,
∵AF、CF是角平分线,
∴∠FAC+∠FCA=45°,
∴∠AFC=180°-45°=135°.
易证△AFC≌△DFC(SAS),
∴∠AFC=∠DFC=135°,
∴∠ADF=90°,
同理可得∠EFC=90°,
∴∠MFN=360°-90°-90°-135°=45°.
∵∠PFM+∠MFN=90°,∠MFN+∠QFG=90°,
∴∠PMF=∠QFG,
∵∠FPM=∠FQG=90°,FP=FQ,
∴△FPM≌△FQG(ASA),
∴PM=QG,FM=FG.
在△FMN和△FGN中
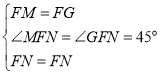
∴△FMN≌△FGN(SAS),
∴MN=NG,
∴MN=NG=NQ+QG=PM+QN,
∴△BMN的周长为:
BM+BN+MN
= BM+BN+ PM+QN
=BP+BQ
=3+3
=6.
故答案为:6.

练习册系列答案
相关题目