题目内容
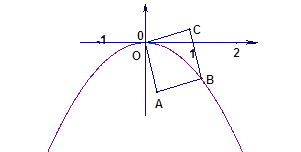
【题目】小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD, BE,当他将一个等腰直角三角板ABC如图垂直放入时,直角顶点C正好在水平线DE上,锐角顶点A和B分别与木墙的顶端重合,求两堵木墙之间的距离。

【答案】两堵木墙之间的距离为20cm.
【解析】
根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可,利用全等三角形的性质进行解答.
由题意得AC=BC,∠ACB=90%,AD⊥ DE,BE⊥DE,
∴∠ADC=∠CEB = 90°,
∴∠ACD+∠BCE=90°, ∠ACD+∠DAC= 90°,
∴∠BCE=∠DAC,
在![]() 和
和![]() 中,
中,

∴![]() ;
;
由题意得:AD= EC=6cm,DC= BE= 14 cm,
∴DE= DC+CE= 20 (cm),
∴两堵木墙之间的距离为20cm.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目