题目内容
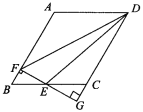
【题目】已知:如图,□ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B点重合),作EF⊥AB于F,FE,DC的延长线交于点G,设BE=x,△DEF的面积为S.
(1)求证:△BEF∽△CEG;
(2)求用x表示S的函数表达式,并写出x的取值范围;
(3)当E点运动到何处时,S有最大值,最大值为多少?
【答案】(1)见解析;(2)![]() (3)当x=3时,S最大值
(3)当x=3时,S最大值![]() .
.
【解析】
(1) 由∠BFG=∠G=90°,∠BEF=∠CEG,得△BEF∽△CEG;
(2)设BE=x,在平行四边形ABCD中,因为∠BAD=120°所以∠B=60°=∠ECG,又BE=x,EC=3-x,所以EF、CG可利用三角函数求出,即在△EFG中,边和边上的高就为已知,从而求出解析式;
(3)由抛物线的开口方向和对称轴可得,当0<x≤3时,S随x的增大而增大,
所以,当x=3时,即E与C重合时,取最大值.
(1)证明:∵EF⊥AB,AB∥DC,
∴EF⊥DG.
∴∠BFG=∠G=90°.
又∵∠BEF=∠CEG,
∴△BEF∽△CEG;
(2)解:由(1)得DG为△DEF中EF边上的高,设BE=x,
在Rt△BFE中, EF=BEsinB=![]() x.
x.
在Rt△CEG中,CE=3x,GC=(3x)cos60°=![]() ,
,
得DG=DC+GC=![]() ,
,
所以,S=![]() EFDG=
EFDG=![]() x2+
x2+![]() x,(其中0<x≤3);
x,(其中0<x≤3);
(3)解:∵a=![]() <0,对称轴x=
<0,对称轴x=![]() >3,
>3,
∴当0<x≤3时,S随x的增大而增大,
所以,当x=3时,即E与C重合时,取最大值S最大值=3![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目