题目内容
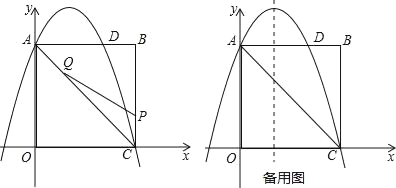
【题目】如图,抛物线y=-x2+bx+c的顶点为C,对称轴为直线x=1,且经过点A(3,-1),与y轴交于点B.
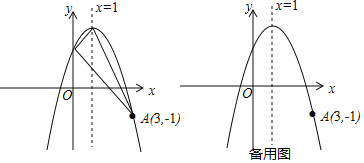
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)经过点A的直线交抛物线于点P,交x轴于点Q,若S△OPA=2S△OQA,试求出点P的坐标.
【答案】(1)y=-x2+2x+2;(2)详见解析;(3)点P的坐标为(1+![]() ,1)、(1-
,1)、(1-![]() ,1)、(1+
,1)、(1+![]() ,-3)或(1-
,-3)或(1-![]() ,-3).
,-3).
【解析】
(1)根据题意得出方程组,求出b、c的值,即可求出答案;
(2)求出B、C的坐标,根据点的坐标求出AB、BC、AC的值,根据勾股定理的逆定理求出即可;
(3)分为两种情况,画出图形,根据相似三角形的判定和性质求出点PE的长,即可得出答案.
解:(1)由题意得: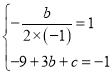 ,
,
解得:![]() ,
,
∴抛物线的解析式为y=-x2+2x+2;
(2)∵由y=-x2+2x+2得:当x=0时,y=2,
∴B(0,2),
由y=-(x-1)2+3得:C(1,3),
∵A(3,-1),
∴AB=3![]() ,BC=
,BC=![]() ,AC=2
,AC=2![]() ,
,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∴△ABC是直角三角形;
(3)①如图,当点Q在线段AP上时,
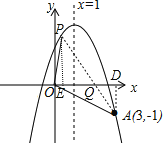
过点P作PE⊥x轴于点E,AD⊥x轴于点D
∵S△OPA=2S△OQA,
∴PA=2AQ,
∴PQ=AQ
∵PE∥AD,
∴△PQE∽△AQD,
∴![]() =
=![]() =1,
=1,
∴PE=AD=1
∵由-x2+2x+2=1得:x=1![]() ,
,
∴P(1+![]() ,1)或(1-
,1)或(1-![]() ,1),
,1),
②如图,当点Q在PA延长线上时,
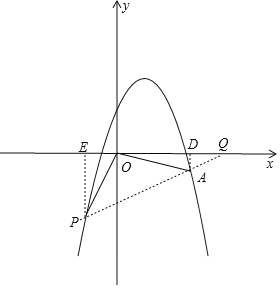
过点P作PE⊥x轴于点E,AD⊥x轴于点D
∵S△OPA=2S△OQA,
∴PA=2AQ,
∴PQ=3AQ
∵PE∥AD,
∴△PQE∽△AQD,
∴![]() =
=![]() =3,
=3,
∴PE=3AD=3
∵由-x2+2x+2=-3得:x=1±![]() ,
,
∴P(1+![]() ,-3),或(1-
,-3),或(1-![]() ,-3),
,-3),
综上可知:点P的坐标为(1+![]() ,1)、(1-
,1)、(1-![]() ,1)、(1+
,1)、(1+![]() ,-3)或(1-
,-3)或(1-![]() ,-3).
,-3).

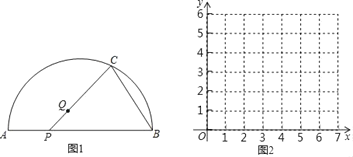
【题目】如图,点P是![]() 所对弦AB上一动点,点Q是
所对弦AB上一动点,点Q是![]() 与弦AB所围成的图形的内部的一定点,作射线PQ交
与弦AB所围成的图形的内部的一定点,作射线PQ交![]() 于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,B,C两点间的距离为y2cm.(当点P与点A重合时,x的值为0).
于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,B,C两点间的距离为y2cm.(当点P与点A重合时,x的值为0).
小平根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小平的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.37 | 4.06 | 2.83 | m | 3.86 | 4.83 | 5.82 |
y2/cm | 2.68 | 3.57 | 4.90 | 5.54 | 5.72 | 5.79 | 5.82 |
经测量m的值是(保留一位小数).
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(3)结合函数图象,解决问题:当△BCP为等腰三角形时,AP的长度约为 cm.