题目内容
【题目】对于平面直角坐标系xOy中的图形W和点P,给出如下定义:F为图形W上任意一点,将P,F两点间距离的最小值记为m,最大值记为M,称M与m的差为点P到图形W的“差距离”,记作d(P,W),即d(P,W)=M-m,已知点A(2,1),B(-2,1)
(1)求d(O,AB);
(2)点C为直线y=1上的一个动点,当d(C,AB)=1时,点C的横坐标是 ;
(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点,当d(D,AB)≤2时,直接写出b的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)画出图形,根据点P到图形W的“差距离”的定义即可解决问题.
(2)如图2中,设C(m,1).由此构建方程即可解决问题.
(3)如图3中,取特殊位置当b=6时,当b=-4时,分别求解即可解决问题.
解:(1)如图1中,

∵A(2,1),B(-2,1),
∴AB∥x轴,
∴点O到线段AB的最小距离为1,最大距离为![]() ,
,
∴d(O,AB)=![]() -1.
-1.
(2)如图2中,设C(m,1).
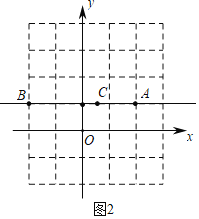
由题意:m-(-2)-(2-m)=1或2-m-[m-(-2)]=1
解得m=![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.
(3)如图3中,

当b=6时,线段EF:y=x+6(-2≤x≤2)上任意一点D,满足d(D,AB)≤2,
当b=-4时,线段E′F′:y=x-4(-2≤x≤2)上任意一点D′,满足d(D′,AB)≤2,
观察图象可知:当b≥6或b≤-4时,函数y=x+b(-2≤x≤2)图象上的任意一点,满足d(D,AB)≤2.

练习册系列答案
相关题目