题目内容
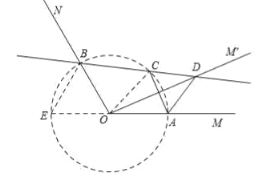
【题目】如图,已知![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() ,将射线
,将射线![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为
,旋转角为![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,画直线
,画直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,有下列结论:
,有下列结论:
①![]() ; ②
; ②![]() 的大小随着
的大小随着![]() 的变化而变化;
的变化而变化;
③当![]() 时,四边形
时,四边形![]() 为菱形; ④
为菱形; ④![]() 面积的最大值为
面积的最大值为![]() ;
;

其中正确的是_____________.(把你认为正确结论的序号都填上).
【答案】①③④
【解析】
①根据对称的性质:对称点的连线被对称轴垂直平分可得:OM'是AC的垂直平分线,再由垂直平分线的性质可作判断;
②作⊙O,根据四点共圆的性质得:∠ACD=∠E=60°,说明∠ACD是定值,不会随着α的变化而变化;
③当α=30°时,即∠AOD=∠COD=30°,证明△AOC是等边三角形和△ACD是等边三角形,得OC=OA=AD=CD,可作判断;
④先证明△ACD是等边三角形,当AC最大时,△ACD的面积最大,当AC为直径时最大,根据面积公式计算后可作判断.
解:①∵A、C关于直线OM'对称,
∴OM'是AC的垂直平分线,
∴CD=AD,
故①正确;
②连接OC,由①知:OM'是AC的垂直平分线,
∴OC=OA,
∴OA=OB=OC,
以O为圆心,以OA为半径作⊙O,交AO的延长线于E,连接BE,
则A、B、C都在⊙O上,
∵∠MON=120°,
∴∠BOE=60°,
∵OB=OE,
∴△OBE是等边三角形,
∴∠E=60°,
∵A、C、B、E四点共圆,
∴∠ACD=∠E=60°,
故②不正确;
③当α=30°时,即∠AOD=∠COD=30°,
∴∠AOC=60°,
∴△AOC是等边三角形,
∴∠OAC=60°,OC=OA=AC,
由①得:CD=AD,
∴∠CAD=∠ACD=∠CDA=60°,
∴△ACD是等边三角形,
∴AC=AD=CD,
∴OC=OA=AD=CD,
∴四边形OADC为菱形,
故③正确;
④∵CD=AD,∠ACD=60°,
∴△ACD是等边三角形,
当AC最大时,△ACD的面积最大,
∵AC是⊙O的弦,即当AC为直径时最大,此时AC=2OA=2a,α=90°,
∴△ACD面积的最大值是:![]() AC2=
AC2=![]() ,
,
故④正确;
所以本题结论正确的有:①③④,
故答案为:①③④.