题目内容
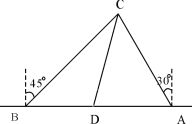
【题目】如图，D为AB上一点，△ACE≌△BCD，AD2+DB2=DE2，试判断△ABC的形状，并说明理由．
【答案】△ABC是等腰直角三角形，理由见解析.
【解析】试题分析：根据全等三角形的性质得出AC=BC，∠EAC=∠B，AE=BD，根据勾股定理的逆定理得出∠EAD=90°，求出∠ACB=90°，即可求出答案．
试题解析：△ABC是等腰直角三角形，
理由是：∵△ACE≌△BCD，
∴AC=BC，∠EAC=∠B，AE=BD，
∵AD2+DB2=DE2，
∴AD2+AE2=DE2，
∴∠EAD=90°，
∴∠EAC+∠DAC=90°，
∴∠DAC+∠B=90°，
∴∠ACB=180°﹣90°=90°，
∵AC=BC，
∴△ABC是等腰直角三角形．
练习册系列答案
特高级教师点拨系列答案
相关题目
