题目内容
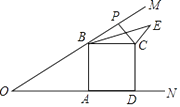
【题目】如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=![]() ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )
﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
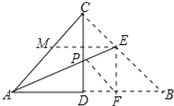
【解析】试题解析:①正确.作EM∥AB交AC于M.
∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵∠CAE=∠BAE=![]() ∠CAB=22.5°,
∠CAB=22.5°,
∴∠MEA=∠EAB=22.5°,
∴∠CME=45°=∠CEM,设CM=CE=a,则ME=AM=![]() a,
a,
∴tan∠CAE=![]() ,故①正确,
,故①正确,
②正确.△CDA≌△CDB,△AEC≌△AEF,△APC≌△APF,△PEC≌△PEF,故②正确,
③正确.∵△PEC≌△PEF,
∴∠PCE=∠PFE=45°,
∵∠EFA=∠ACE=90°,
∴∠PFA=∠PFE=45°,
∴若将△PEF沿PF翻折,则点E一定落在AB上,故③正确.
④正确.∵∠CPE=∠CAE+∠ACP=67.5°,∠CEP=90°﹣∠CAE=67.5°,
∴∠CPE=∠CEP,
∴CP=CE,故④正确,
⑤错误.∵△APC≌△APF,
∴S△APC=S△APF,
假设S△APF=S四边形DFPE,则S△APC=S四边形DFPE,
∴S△ACD=S△AEF,
∵S△ACD=![]() S△ABC,S△AEF=S△AEC≠
S△ABC,S△AEF=S△AEC≠![]() S△ABC,
S△ABC,
∴矛盾,假设不成立.
故⑤错误.
 .
.
故选C.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】某人购进一批苹果到市场上零售,已知卖出苹果数量x与售价y的关系如下表.
数量x(千克) | 1 | 2 | 3 | 4 | 5 |
售价y(元) | 3+0.1 | 6+0.2 | 9+0.3 | 12+0.4 | 15+0.5 |
则当卖出苹果数量为10千克时,售价y为_______元.