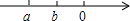题目内容
已知a，b，c在数轴上的位置如下图，化简代数式
-|a+b|+
+|b+c|的值．
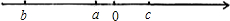
| a2 |
| (c-a)2 |
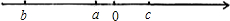
根据数轴可以得到：b＜a＜0＜c，且|b|＞|c|，
∴a+b＜0，c-a＞0，b+c＜0，
∴
-|a+b|+
+|b+c|
=|a|-|a+b|+|c-a|+|b+c|
=-a+（a+b）+（c-a）-（b+c）
=-a+a+b+c-a-b-c
=-a．
故答案为：-a．
∴a+b＜0，c-a＞0，b+c＜0，
∴
| a2 |
| (c-a)2 |
=|a|-|a+b|+|c-a|+|b+c|
=-a+（a+b）+（c-a）-（b+c）
=-a+a+b+c-a-b-c
=-a．
故答案为：-a．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
