题目内容
【题目】定义:我们把三角形被一边中线分成的两个三角形叫做“朋友三角形”.
性质:“朋友三角形”的面积相等.
如图1,在△ABC中,CD是AB边上的中线.
那么△ACD和△BCD是“朋友三角形”,并且S△ACD=S△BCD .
应用:如图2,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=AD=4,BC=6,点E在BC上,点F在AD上,BE=AF,AE与BF交于点O.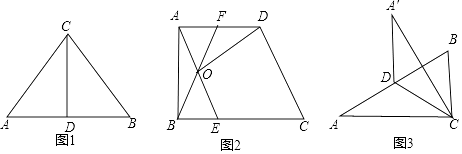
(1)求证:△AOB和△AOF是“朋友三角形”;
(2)连接OD,若△AOF和△DOF是“朋友三角形”,求四边形CDOE的面积.
拓展:如图3,在△ABC中,∠A=30°,AB=8,点D在线段AB上,连接CD,△ACD和△BCD是“朋友三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的 ![]() ,则△ABC的面积是(请直接写出答案).
,则△ABC的面积是(请直接写出答案).
【答案】
(1)
证明:∵AD∥BC,
∴∠OAF=∠OEB,
在△AOF和△EOB中, 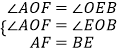 ,
,
∴△AOF≌△EOB(AAS),
∴OF=OB,
则AO是△ABF的中线.
∴△AOB和△AOF是“朋友三角形”
(2)8或8 ![]()
【解析】(2)解:∵△AOF和△DOF是“朋友三角形”,
∴S△AOF=S△DOF ,
∵△AOF≌△EOB,
∴S△AOB=S△EOB ,
∵△AOB和△AOF是“朋友三角形”
∴S△AOB=S△AOF ,
∴S△AOF=S△DOF=S△AOB=S△EOB , = ![]() ×4×2=4,
×4×2=4,
∴四边形CDOE 的面积=S梯形ABCD﹣2S△ABE= ![]() ×(4+6)×4﹣2×4=12;
×(4+6)×4﹣2×4=12;
拓展:解:分为两种情况:①如图1所示: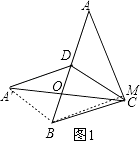
∵S△ACD=S△BCD .
∴AD=BD= ![]() AB=4,
AB=4,
∵沿CD折叠A和A′重合,
∴AD=A′D= ![]() AB=
AB= ![]() ×8=4,
×8=4,
∵△A′CD与△ABC重合部分的面积等于△ABC面积的 ![]() ,
,
∴S△DOC= ![]() S△ABC=
S△ABC= ![]() S△BDC=
S△BDC= ![]() S△ADC=
S△ADC= ![]() S△A′DC ,
S△A′DC ,
∴DO=OB,A′O=CO,
∴四边形A′DCB是平行四边形,
∴BC=A′D=4,
过B作BM⊥AC于M,
∵AB=8,∠BAC=30°,
∴BM= ![]() AB=4=BC,
AB=4=BC,
即C和M重合,
∴∠ACB=90°,由勾股定理得:AC= ![]() =4
=4 ![]() ,
,
∴△ABC的面积= ![]() ×BC×AC=
×BC×AC= ![]() ×4×4
×4×4 ![]() =8
=8 ![]() ;
;
②如图2所示: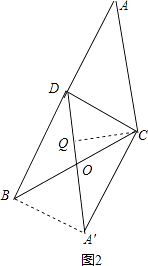
∵S△ACD=S△BCD .
∴AD=BD= ![]() AB,
AB,
∵沿CD折叠A和A′重合,
∴AD=A′D= ![]() AB=
AB= ![]() ×8=4,
×8=4,
∵△A′CD与△ABC重合部分的面积等于△ABC面积的 ![]() ,
,
∴S△DOC= ![]() S△ABC=
S△ABC= ![]() S△BDC=
S△BDC= ![]() S△ADC=
S△ADC= ![]() S△A′DC ,
S△A′DC ,
∴DO=OA′,BO=CO,
∴四边形A′BDC是平行四边形,
∴A′C=BD=4,
过C作CQ⊥A′D于Q,
∵A′C=4,∠DA′C=∠BAC=30°,
∴CQ= ![]() A′C=2,
A′C=2,
∴S△ABC=2S△ADC=2S△A′DC=2× ![]() ×A′D×CQ=2×
×A′D×CQ=2× ![]() ×4×2=8;
×4×2=8;
即△ABC的面积是8或8 ![]() ;
;
所以答案是:8或8 ![]() .
.