题目内容
【题目】如图,一次函数y1=kx+b的图象与x轴、y轴分别交于点A、B,与一次函数y2=x的图象交于点M,点A的坐标为(6,0),点M的横坐标为2,过点P(a,0),作x轴的垂线,分别交函数y=kx+b和y=x的图象于点C、D. 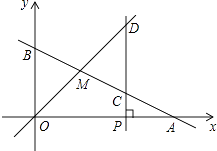
(1)求一次函数y1=kx+b的表达式;
(2)若点M是线段OD的中点,求a的值.
【答案】
(1)解:∵M的横坐标为2,点M在直线y=x上,
∴y=2,
∴M(2,2)
把M(2,2)、A(6,0)代入y1=kx+b中,
可得: ![]() ,
,
解得: 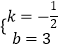
∴函数的表达式为:y1=﹣ ![]() x+3
x+3
(2)解:∵PD⊥x轴,
∴PC∥OB
∴∠BOM=∠CDM,
∵点M是线段CD的中点,
∴MO=MD
在△MBO与△MCD中
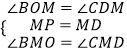
∴△MBO≌△MCD(ASA)
∴OB=CD
当x=0时,
y1= ![]() x+3=3,
x+3=3,
∴OB=2,
∴DC=3,
当x=a时,
y1=﹣ ![]() x+3=3﹣
x+3=3﹣ ![]() a,
a,
∴y2=x=a
即D(a,a),C(a,﹣ ![]() a+3)
a+3)
∴DC=a﹣(﹣ ![]() a+3)=
a+3)= ![]() a﹣3=3,
a﹣3=3,
∴a=4
【解析】(1)先求出M的坐标,然后将M与A的坐标代入y1=kx+b中,即可求出k与b的值.(2)根据条件先证明△MBO≌△MCD(ASA),由此可知OB=CD,分别求出OB与CD的长度即可求出a的值.

练习册系列答案
相关题目