题目内容
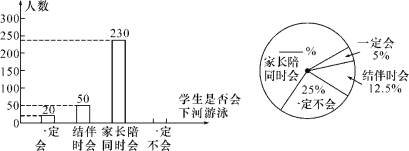
【题目】某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间t(h)与行驶速度v(km/h)满足反比例函数关系,其图象为如图所示的一段曲线.且端点为A(40,1)和B(m,0.5).
(1)求t与v的函数关系式及m的值;
(2)若该段公路限速50km/h,求通过该路段需要的最短时间和这段公路的长.
【答案】
(1)解:由题意,可设t与v的函数关系式为t= k v (k≠0),
∵函数t= ![]() 经过点A(40,1),
经过点A(40,1),
∴1= ![]() ,解得k=40,
,解得k=40,
∴t与v的函数关系式为t= ![]() ;
;
把B(m,0.5)代入t= ![]() ,
,
得0.5= ![]() ,解得m=80
,解得m=80
(2)解:把v=50代入t= ![]() ,得t=
,得t= ![]() =0.8,
=0.8,
则通过该路段需要的最短时间是0.8小时,这段公路的长为40km.
【解析】利用图像寻找一点坐标代入解析式即可;(2)将v=50代入反比例函数解析式即可.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目