题目内容
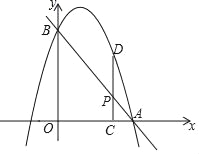
【题目】如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
【答案】(1)①点N坐标为(![]() ,3);②不存在.理由见解析;(2)存在.满足条件的抛物线的解析式为y=﹣2x2+2x+4或y=﹣
,3);②不存在.理由见解析;(2)存在.满足条件的抛物线的解析式为y=﹣2x2+2x+4或y=﹣![]() x2+3x+4.
x2+3x+4.
【解析】
(1)①将抛物线配成顶点式可得到顶点坐标M![]() 再通过
再通过![]() 在对称轴上求出N的坐标;
在对称轴上求出N的坐标;
②易得![]() ,通过将点P,点D的坐标设出来可得
,通过将点P,点D的坐标设出来可得![]() ,由PD∥MN,可知PD=MN时,四边形MNPD是平行四边形;求
,由PD∥MN,可知PD=MN时,四边形MNPD是平行四边形;求![]() 值后通过比较
值后通过比较![]() 与
与![]() 的大小可判断四边形MNPD是否为菱形;
的大小可判断四边形MNPD是否为菱形;
(2)先由点P的坐标求出![]() ,然后将抛物线解析式设为y=ax2+bx+4,再由
,然后将抛物线解析式设为y=ax2+bx+4,再由![]() 得到
得到![]() ,求出
,求出![]() 由∠DPB=∠OBA,可对相似三角形进行分类讨论,分别求出
由∠DPB=∠OBA,可对相似三角形进行分类讨论,分别求出![]() 值即可.
值即可.
(1)①如图1,
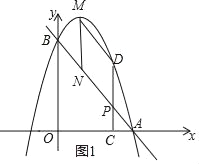
![]()
∴顶点为M的坐标为![]()
当![]() 时,
时,![]() ,则点N坐标为
,则点N坐标为![]()
②不存在.
理由如下:
![]()
设P点坐标为![]() ,则
,则![]()
∴![]()
∵PD∥MN,
当PD=MN时,四边形MNPD为平行四边形,即![]() 解得
解得![]() (舍去),
(舍去),![]() 此时P点坐标为
此时P点坐标为![]()
∵![]()
∴PN≠MN,
∴平行四边形MNPD不为菱形,
∴不存在点P,使四边形MNPD为菱形;
(2)存在.
如图2,
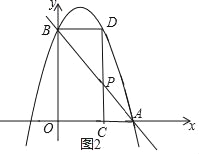
OB=4,OA=2,则![]()
当x=1时,y=﹣2x+4=2,则P(1,2),
∴![]()
设抛物线的解析式为y=ax2+bx+4,
把A(2,0)代入得4a+2b+4=0,解得b=﹣2a﹣2,
∴抛物线的解析式为y=ax2﹣2(a+1)x+4,
当x=1时,y=ax2﹣2(a+1)x+4=a﹣2a﹣2+4=2﹣a,则D(1,2﹣a),
∴![]()
∵DC∥OB,
∴∠DPB=∠OBA,
∴当![]() 时,△PDB∽△BOA,即
时,△PDB∽△BOA,即![]() ,解得
,解得![]() ,此时抛物线解析式为
,此时抛物线解析式为![]()
当![]() 时,△PDB∽△BAO,即
时,△PDB∽△BAO,即![]() ,解得
,解得![]() ,此时抛物线解析式为
,此时抛物线解析式为![]()
综上所述,满足条件的抛物线的解析式为![]() 或
或![]()