题目内容
【题目】如图,在六边形的顶点处分别标上数1, 2, 3, 4,5, 6,能否使任意三个相邻顶点处的三个数之和
（1）大于9?
（2）大于10?如能,请在图中标出来;若不能,请说明理由.
【答案】
（1）
解：(1) 可设符合条件的一组数是1，a1,a2,a3,a4,a5，其中1与a5相邻，
则a1+a2≥9，a4+a5≥9，明显a1,a2,a3,a4都不为2，只当a1,a2,a4,a5分别为6，3,5,4时符合，即为1，6，3，2，5，4.
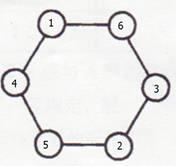
（2）
解：这六个数的平均数是3.5,三倍之后是10.5.
如果能的话,相邻三数之和至少要是11,所以六个数的平均值至少要是 
，3.5显然不够大,所以排不出来.
【解析】（1）以1为基础相两边填数，由题意可得在1两边连续的两个数的和要大于或等于9，即可有6+3=4+5=9符合；（2）最大的三相邻数和也只有11,是满足本题要求的最起码条件,所以已经无提升空间,也证明了本题不可行.
【考点精析】关于本题考查的数与式的规律，需要了解先从图形上寻找规律，然后验证规律，应用规律，即数形结合寻找规律才能得出正确答案．
练习册系列答案
相关题目
【题目】某商场销售A，B两种品牌的教学设备，这两种教学设备的进价和售价如表所示：
A | B | |
进价（万元/套） | 1.5 | 1.2 |
售价（万元/套） | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套，共需66万元，全部销售后可获毛利润9万元．[毛利润=（售价﹣进价）×销售量]
（1）该商场计划购进A，B两种品牌的教学设备各多少套？
（2）通过市场调研，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少的数量的1.5倍．若用于购进这两种教学设备的总资金不超过69万元，问A种设备购进数量至多减少多少套？
