题目内容
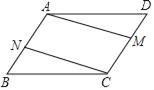
【题目】如图,在四边形ABCD中,AB∥CD,AD∥BC,AN=CM.
(1)求证:BN=DM;
(2)若BC=3,CD=2,∠B=50°,求∠BCD、∠D的度数及四边形ABCD的周长.
【答案】(1)证明见解析;(2)∠BCD=130°,∠D=50°,四边形ABCD的周长=10.
【解析】
(1)首先判断四边形ABCD和四边形ANMD为平行四边形,然后由“平行四边形的对边相等”推知AB=CD,AN=CM,由等式的性质证得结论;
(2)根据平行四边形的对边平行,平行线的性质以及平行四边形的对角相等进行解答.
(1)∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴AB=CD,
又∵AN=CM,
∴四边形ANMD为平行四边形,
∴AN=CM,
∴AB﹣AN=CD﹣CM,即BN=DM;
(2)∵AB∥CD,
∴∠B+∠BCD=180°,
∵∠B=50°,
∴∠BCD=180°﹣50°=130°,
由(1)知,四边形ABCD是平行四边形,
∴∠D=∠B=50°,AB=CD,AD=BC,
∵BC=3,CD=2,
∴四边形ABCD的周长=2(BC+CD)=2×(3+2)=10.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目