Question

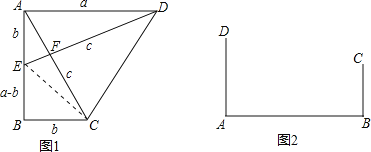
【题目】如图，用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD，中间是空的小正方形EFGH．若AB=a，EF=b，判断以下关系式：① x + y=a；② x－y=b；③ a2－b2=2xy；④ x2－y2=ab；⑤ x2 + y2=，其中正确的有__________.

Answer 1

【答案】①②④⑤

【解析】

利用大正方形的边长=长方形的长+长方形的宽，小正方形的边长=长方形的长-长方形的宽，大正方形的面积-小正方形的面积=4个长方形的面积，完全平方公式x2+y2=（x+y）2-2xy，进而判定即可．

由图形可得：①大正方形的边长=长方形的长+长方形的宽，故x+y=a正确；

②小正方形的边长=长方形的长-长方形的宽，故x-y=b正确；

③大正方形的面积-小正方形的面积=4个长方形的面积，故a2-b2=4xy错误；

④根据①知x+y=a，根据②知x-y=b，则x2-y2=ab，正确；

⑤x2+y2=（x+y）2-2xy=a2-2×，正确．

所以正确的是①②④⑤．

故答案为：①②④⑤．