题目内容
【题目】如图1，已知矩形ABCD的宽AD=8，点E在边AB上，P为线段DE上的一动点（点P与点D，E不重合），∠MPN=90°，M，N分别在直线AB，CD上，过点P作直线HK 
AB，作PF⊥AB，垂足为点F，过点N作NG⊥HK，垂足为点G
（1）求证：∠MPF=∠GPN
（2）在图1中，将直角∠MPN绕点P顺时针旋转，在这一过程中，试观察、猜想：当MF=NG时，△MPN是什么特殊三角形？在图2中用直尺画出图形，并证明你的猜想；
（3）在（2）的条件下，当∠EDC=30°时，设EP＝ｘ，△MPN的面积为S，求出S关于ｘ的解析式，并说明S是否存在最小值？若存在，求出此时ｘ的值和△MPN面积的最小值；若不存在，请说明理由。
【答案】
（1）证明：∵直线HK∥AB，PF⊥AB，
∴PF⊥HK，
∴∠MDF+∠MPG=∠MPG+∠GPM=90°，
∴∠MPF=∠GPN；
（2）证明：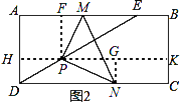 
∵MF=NG，∠MFP=∠NGP=90°，
由（1）得∠MPF=∠GPN，
∴△MFP和△NGP中，
，
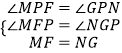∴△MFP≌△△NGP，
∴MP=NP，则△MPN是等腰三角形；
（3）解：△MPN面积存在最小值，此时x=8，S的最小值是16．
∵∠EDG=30°，∠PEF=30°，EP=x，
∴PF= 
，
根据题意得：PF+NG=8，
∴NG=8- ，
由（2）可得MF=NG=8- ，
在直角△PMF中，PF2+MF2=PM2，
则PM2=（ ）2+（8- ）2= 
-8x+6，
∵△MPN的面积是S= 
PM2，
∴S= PM2= 
-4x+32= 
（x-8）2+16，
又∵0＜x＜16，
∴当x=8时，△MPN的面积S的最小值是16．
【解析】（1）矩形中含有直角，所以求角相等是可以考虑用互余关系∠MDF+∠MPG=∠MPG+∠GPM=90°，得到∠MPF=∠GPN；
（2）对于猜想题很容易由图像猜到为等腰直角三角形，再由第一问得到的角相等∠MPF=∠GPN，易证△MFP≌△NGP得到MP=NP，则△MPN是等腰三角形。
（3）由30°所对的直角边等于斜边的一半，易得PF= ,再由等量代换可得MF=NG=8- ，再由勾股定理求得 PM2=（ ）2+（8- ）2= -8x+6最终由二次函数顶点坐标得到最值。
