题目内容
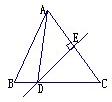
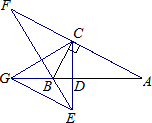 在△ABC中,∠C=90°,∠CBA的外角平分线,交AC的延长线于F,交斜边上的高CD的延长线于E,EG∥AC交AB的延长线于G,则下列结论:①CF=CE;②GE=CF;③EF是CG的垂直平分线;④BC=BG.其中正确的是
在△ABC中,∠C=90°,∠CBA的外角平分线,交AC的延长线于F,交斜边上的高CD的延长线于E,EG∥AC交AB的延长线于G,则下列结论:①CF=CE;②GE=CF;③EF是CG的垂直平分线;④BC=BG.其中正确的是
- A.①②③④
- B.①③④
- C.②③④
- D.①②
A
分析:由BF平分∠GBC得∠GBF=∠CBF,易得∠CBF=∠EBD,利用等角的余角相等得到∠F=∠BED,利用等腰三角形的性质即可得到①正确;由GE∥AF,利用平行线的性质得∠F=∠GEB,则∠GEB=∠CEB,易证△BEG≌△BEC,则GE=CE,即可得到②正确;根据等腰三角形的性质易得EB垂直平分GC,所以③正确;根据垂直平分线的性质得BG=BC,所以④正确.
解答: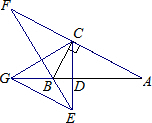 解:∵BF平分∠GBC,
解:∵BF平分∠GBC,
∴∠GBF=∠CBF,
而∠GBF=∠EBD,
∴∠CBF=∠EBD,
∵∠BCA=90°,CD为高,
∴∠F=∠BED,
∴CF=CE,所以①正确;
又∵GE∥AF,
∴∠F=∠GEB,
∴∠GEB=∠CEB,
而∠GBF=∠CBF,
∴∠GBE=∠CBE,
BE公共,
∴△BEG≌△BEC,
∴GE=CE,
∴GE=CF,所以②正确;
在△EGC中,
EC=EG,BE平分∠CEG,
∴EB垂直平分GC,所以③正确;
∴BG=BC,所以④正确.
故选A.
点评:本题考查了全等三角形的判定与性质:有两组对应角相等,且它们的夹边也相等的两个三角形全等;全等三角形的对应边相等.也考查了等腰三角形的性质以及垂直平分线的性质.
分析:由BF平分∠GBC得∠GBF=∠CBF,易得∠CBF=∠EBD,利用等角的余角相等得到∠F=∠BED,利用等腰三角形的性质即可得到①正确;由GE∥AF,利用平行线的性质得∠F=∠GEB,则∠GEB=∠CEB,易证△BEG≌△BEC,则GE=CE,即可得到②正确;根据等腰三角形的性质易得EB垂直平分GC,所以③正确;根据垂直平分线的性质得BG=BC,所以④正确.
解答:
 解:∵BF平分∠GBC,
解:∵BF平分∠GBC,∴∠GBF=∠CBF,
而∠GBF=∠EBD,
∴∠CBF=∠EBD,
∵∠BCA=90°,CD为高,
∴∠F=∠BED,
∴CF=CE,所以①正确;
又∵GE∥AF,
∴∠F=∠GEB,
∴∠GEB=∠CEB,
而∠GBF=∠CBF,
∴∠GBE=∠CBE,
BE公共,
∴△BEG≌△BEC,
∴GE=CE,
∴GE=CF,所以②正确;
在△EGC中,
EC=EG,BE平分∠CEG,
∴EB垂直平分GC,所以③正确;
∴BG=BC,所以④正确.
故选A.
点评:本题考查了全等三角形的判定与性质:有两组对应角相等,且它们的夹边也相等的两个三角形全等;全等三角形的对应边相等.也考查了等腰三角形的性质以及垂直平分线的性质.

练习册系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
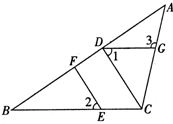 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.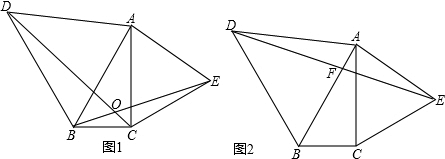
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于