题目内容
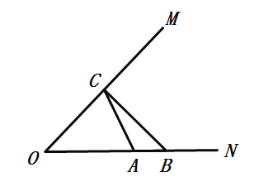
【题目】如图,已知![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 是边
是边![]() 上一个动点,若
上一个动点,若![]() 周长的最小值是6,则
周长的最小值是6,则![]() 的长是( )
的长是( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
【答案】D
【解析】
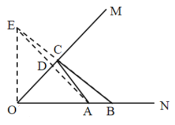
作点A关于OM的对称点E,AE交OM于点D,连接BE、OE,BE交OM于点C,此时△ABC周长最小,根据题意及作图可得出△OAD是等腰直角三角形,OA=OE=3,,所以∠OAE=∠OEA=45°,从而证明△BOE是直角三角形,然后设AB=x,则OB=3+x,根据周长最小值可表示出BE=6-x,最后在Rt△OBE中,利用勾股定理建立方程求解即可.
解:作点A关于OM的对称点E,AE交OM于点D,连接BE、OE,BE交OM于点C,
此时△ABC周长最小,最小值=AB+AC+BC=AB+EC+BC=AB+BE,
∵△ABC周长的最小值是6,
∴AB+BE=6,
∵∠MON=45°,AD⊥OM,
∴△OAD是等腰直角三角形,∠OAD=45°,
由作图可知OM垂直平分AE,
∴OA=OE=3,
∴∠OAE=∠OEA=45°,
∴∠AOE=90°,
∴△BOE是直角三角形,
设AB=x,则OB=3+x,BE=6-x,
在Rt△OBE中,![]() ,
,
解得:x=1,
∴AB=1.
故选D.

练习册系列答案
相关题目
【题目】某弹簧挂上不超过20千克的物体后按一定规律伸长,测得一弹簧的长度![]() (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量![]() (千克)有下面的关系:
(千克)有下面的关系:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
那么弹簧的总长![]() (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量![]() (千克)之间是否是函数关系?若是,请写出函数关系式.
(千克)之间是否是函数关系?若是,请写出函数关系式.