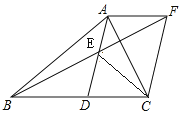
题目内容
【题目】某餐厅中1张餐桌可坐6人,有以下两种摆放方式:
(1)对于方式一:4张桌子拼在一起可坐 人;对于方式二,n张桌子拼在一起可坐 人;
(2)该餐厅有40张这样的长方形桌子,若按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)在(2)中,若改成每8张拼成一张大桌子,按方式二的拼法,则40张桌子共可坐多少人?
(4)一天中午,该餐厅来了98位顾客共同就餐,要求用满座位,但餐厅中只有25张这样的长方形桌子可用,若你是这家餐厅的经理,你打算选择哪种方式来摆餐桌呢(不考虑场地等因素)?

【答案】(1)18;(2n+4);
(2)按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐176人;
(3)按方式二的拼法,则40张桌子共可坐100人;
(4)按方式一,用21张桌子连拼成一大桌,按方式二,用4张桌子连拼成一大桌,即可坐满98人.
【解析】
(1)根据题意和图形可以解答本题;
(2)根据题意和题目中的数据可以解答本题;
(3)根据题意和题目中的数据可以解答本题;
(4)根据题意可以写出相应的方案,本题答案不唯一,只要符合题意即可.
(1)对于方式一:4张桌子拼在一起可坐2+4×4=18(人),
对于方式二,n张桌子拼在一起可坐:(2n+4)人,
故答案为:18;(2n+4);
(2)按方式一,每5张拼成一张大桌子,一个大桌可坐2+4×5=22(人),则拼成8张大桌子可坐22×8=176(人),
答:按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐176人;
(3)按方式二,每8张拼成一张大桌子,一个大桌可坐2×8+4=20(人),则拼成![]() =5张大桌子可坐20×5=100(人),
=5张大桌子可坐20×5=100(人),
答:按方式二的拼法,则40张桌子共可坐100人;
(4)因为一张小桌可坐6人,当n=25时,共坐6×25=150>98,有多空位,
以下是几张小桌拼成一张大桌的座位数列表供
连拼数目座位 | 2张连拼 | 3张连拼 | 4张连拼 | 5张连拼 | 6张连拼 | 8张连拼 |
方式一 | 10 | 14 | 18 | 22 | 26 | 34 |
方式二 | 8 | 10 | 12 | 14 | 16 | 18 |
经分析,用单一方式摆放难以实现要求,所以可考虑两种方式搭配,观察思考可得:
将16张桌子按方式一摆成8张连拼的2个大桌,余下9张桌子按方式二摆成3张连拼的3个大桌,2×34+3×10=98,正好坐满.
(方案不唯一,或用以下方案)
设用x张桌子连拼成一个大桌摆成方式一,则用(25-x)张桌子连拼成一个大桌摆成方式二,则可坐人数为:4x+2+2(25-x)+4=2x+56=98,
可得:x=21,25-x=4,
答:按方式一,用21张桌子连拼成一大桌,按方式二,用4张桌子连拼成一大桌,即可坐满98人.

【题目】在学校组织的“最美数学小报”的评比中,校团委给每个同学的作品打分,成绩分为![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
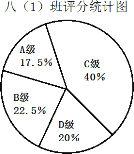

请你根据以上提供的信息解答下列问题:
(1)将表格补充完整.
平均数(分) | 中位数(分) | 众数(分) | |
八(1)班 | 83.75 | 80 | |
八(2)班 | 80 |
(2)若八(1)班有40人,且评分为B级及以上的同学有纪念奖章,请问该班共有几位同学得到奖章?
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买![]() 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?