题目内容
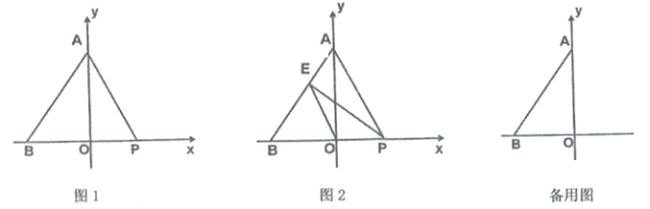
【题目】在Rt△ABC中,AB=6cm,AC=8cm,动点P以3cm/s从点B出发向终点C运动;动点Q以1cm/s从点C出发向终点B运动,动点P,Q同时出发,以PQ为直径在BC上方作半圆O,设运动时间为t(s).
(1)当t=1时,半圆O的半径R=_______;
(2)当半圆O落在△ABC的内部(包括边界)时,求t的取值范围;
(3)当点P在Q的左边时,过点P作PE//AB交半圆于点E.,求tan∠EAC的值.

【答案】(1)3;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)根据题意求出BP、QC的长即可.(2)分类讨论:①当点P在点Q的左侧且半圆O与边AC相切时,可证明△ODC∽△BAC,可知![]() ,根据BP=3t,CQ=t,代入求出t的值即可.;②当点P在点Q的右侧,且半圆O与边AC相切时,同理可证△ODC∽△BAC,PQ=4t-10,可求出CP=10-3t,CO=5-t根据相似三角形各边的比例关系求出t即可.结合两点求出t的取值范围即可.(3)由PE//AB可知△PFC∽△BAC,∠AFP=∠AFC=90°,得
,根据BP=3t,CQ=t,代入求出t的值即可.;②当点P在点Q的右侧,且半圆O与边AC相切时,同理可证△ODC∽△BAC,PQ=4t-10,可求出CP=10-3t,CO=5-t根据相似三角形各边的比例关系求出t即可.结合两点求出t的取值范围即可.(3)由PE//AB可知△PFC∽△BAC,∠AFP=∠AFC=90°,得![]() ,可求出PF、CF的值,进而求出AF的长,连接EQ,同理可求长PE的长,进而求出EF的长,根据正切定义求出tan∠EAC的值即可.
,可求出PF、CF的值,进而求出AF的长,连接EQ,同理可求长PE的长,进而求出EF的长,根据正切定义求出tan∠EAC的值即可.
(1)∵t=1,
∴BP=3,QC=1,
∴PQ=6,R=3.
(2)①当点P在点Q的左侧且半圆O与边AC相切时,
记切点为D,即OD⊥AC
∵∠BAC=Rt∠
∴OD//AB
∴△ODC∽△BAC
∴![]()
∵BP=3t,CQ=t ∴PQ=10-4t即OD=PO=OQ=5-2t
∴CO=5-t
∴![]() ∴
∴![]()

②当点P在点Q的右侧,且半圆O与边AC相切时,
同理得,△ODC∽△BAC,
∴![]()
∵BP=3t,CQ=t ∴PQ=4t-10即OD=PO=OQ=2t-5
∵CP=10-3t
∴CO=5-t
∴![]() ∴
∴![]()

∴![]()
(3)如图所示,PE//AB交AC于点F,连接AE
∴△PFC∽△BAC,∠BAC=∠AFC=90°
∴![]()
∵CP=10-3t
∴![]()
∴![]() ,
,![]()
∴![]()
连接EQ,得∠PEQ=∠PFC=90°
∴EQ//AC
∴△PEQ∽△PFC
同理得![]()
∴![]()
∴![]()