Question

【题目】如图,在平面直角坐标系中，点坐标为，点是轴正半轴上一点，且，点是轴上位于点右侧的一个动点，设点的坐标为．

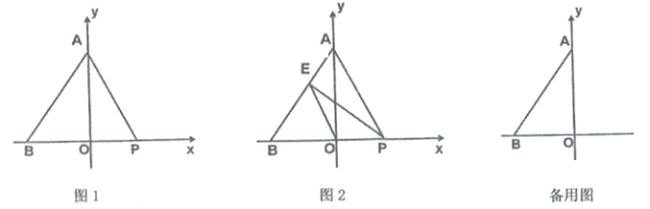
（1）点的坐标为（ ）；

（2）当是等腰三角形时，求点的坐标；

（3）如图2，过点作交线段于点，连接，若点关于直线的对称点为，当点恰好落在直线上时， ．（直接写出答案）

Answer 1

【答案】（1）；（2）或或；（3）

【解析】

（1）利用勾股定理求出OA即可；

（2）分三种情况讨论：①当时，②当时，③当时，分别进行计算即可；

（3）连接OA’， OA与PE交于点C，易得△OEA≌△OEA’，证明∠OA’E＝∠OPC，求出OP＝OA’＝OA＝4，易得∠BEO＝∠PEO，作OG⊥EB于点G，OH⊥EP于点H，可得OG＝OH，然后根据底边上高相等的情况下，面积比等于底边之比求出，再根据勾股定理构建方程即可求出BE.

解：（1）∵，

∴OB=3，

∴OA=，

∴；

（2）当为等腰三角形时，分三种情况讨论：

①当时，

∵，

∴此时；

②当时，

∵，

∴此时；

③当时，设P点坐标为（m，0），

则：，

解得：，

∴此时；

（3）如图，连接OA’， OA与PE交于点C，

∵点关于直线的对称点在直线上，

∴△OEA≌△OEA’，

∴∠OAE＝∠OA’E，OA＝OA’， ∠AEO＝∠A’EO，

∵∠AEC＝∠COP＝90°，∠ACE＝∠OCP，

∴∠OAE＝∠OPC，

∴∠OA’E＝∠OPC，

∴OP＝OA’，

∴OP＝OA＝4，

∴BP＝7，

∵∠AEO＝∠A’EO，∠AEC＝∠A’EB，

∴∠BEO＝∠PEO，

作OG⊥EB于点G，OH⊥EP于点H，

则OG＝OH，

∵，

∴，

设BE=3x，则EP=4x，

∵BE2+EP2=BP2，

∴，

解得：，

∴.