题目内容
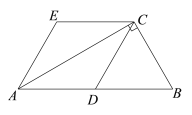
【题目】如图,在Rt△ABC中,∠ACB = 90,D为AB的中点,AE∥DC,CE∥DA.
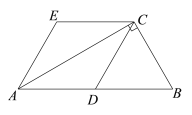
(1)求证:四边形ADCE是菱形;
(2)连接DE,若AC =![]() ,BC =2,求证:△ADE是等边三角形.
,BC =2,求证:△ADE是等边三角形.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)先根据题意证明四边形ADCE是平行四边形,再由直角三角形斜边中线等于斜边的一半可得AD= BD=CD,即可可求证结论;
(2)在Rt△ABC中,由三角函数值可知∠CAB=30,继而根据菱形的性质可知AE = AD,∠EAD=2∠CAB=60,进而即可求证结论.
证明:(1)∵ AE∥DC,CE∥DA,
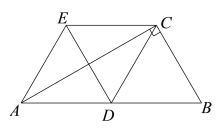
∴ 四边形ADCE是平行四边形.
∵ 在Rt△ABC中, D为AB的中点,
∴ AD= BD=CD=![]() .
.
∴ 四边形ADCE是菱形.
(2)在Rt△ABC中,AC =![]() ,BC =2,
,BC =2,
∴ ![]() .
.
∴ ∠CAB=30.
∵ 四边形ADCE是菱形.
∴ AE = AD,∠EAD=2∠CAB=60.
∴ △ADE是等边三角形.

练习册系列答案
相关题目