题目内容
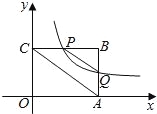
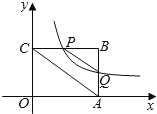
【题目】如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线![]() (x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
(1)若P为边BC的中点,求双曲线的函数表达式及点Q的坐标;
(2)求k的取值范围;
(3)连接PQ,AC,判断:PQ∥AC是否总成立?并说明理由.
【答案】(1)y=![]() ,(4,
,(4,![]() )(2)0<k<12(3)PQ∥AC总成立
)(2)0<k<12(3)PQ∥AC总成立
【解析】
试题分析:(1)先求出点P坐标,再利用待定系数法求出反比例函数解析式,根据点Q的横坐标即可求出点Q的纵坐标.
(2)设点P(x,3),则x=![]() ,列出不等式即可解决问题.
,列出不等式即可解决问题.
(3)根据两边成比例夹角相等的两个三角形相似证明△BPQ∽△BCA,即可解决问题.
试题解析:(1)∵四边形OABC是矩形,
∴BC∥OA,
∵点B坐标(4,3),
∴BC=4,AB=3,
∵PC=PB,
∴点P坐标(2,3),
∴反比例函数解析式y=![]() ,
,
∵点Q的横坐标为4,
∴点Q的坐标为(4,![]() ).
).
(2)设点P坐标(x,3),则0<x<4,
把点P(x,3)代入y=![]() 得到,x=
得到,x=![]() ,
,
∴0<![]() <4,
<4,
∴0<k<12.
(3)结论:PQ∥AC总成立.
理由:设P(m,3),Q(4,n),则3m=4n=k,
∴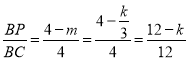 ,
,
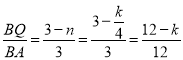 ,
,
∴![]() ,
,
∵∠B=∠B,
∴△BPQ∽△BCA,
∴∠BPQ=∠BCA,
∴PQ∥AC.

练习册系列答案
相关题目